十五周算法训练营——岛屿问题

,给你一个由 ‘1’（陆地）和 ‘0’（水）组成的的二维网格，请你计算网格中岛屿的数量。,岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。,此外，你可以假设该网格的四条边均被水包围。,示例 1：,输入：grid = [ [“1″,”1″,”1″,”1″,”0”], [“1″,”1″,”0″,”1″,”0”], [“1″,”1″,”0″,”0″,”0”], [“0″,”0″,”0″,”0″,”0”] ] 输出：1,给你一个大小为 m x n 的二进制矩阵 grid 。,岛屿 是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0（代表水）包围着。,岛屿的面积是岛上值为 1 的单元格的数目。,计算并返回 grid 中最大的岛屿面积。如果没有岛屿，则返回面积为 0 。,示例 1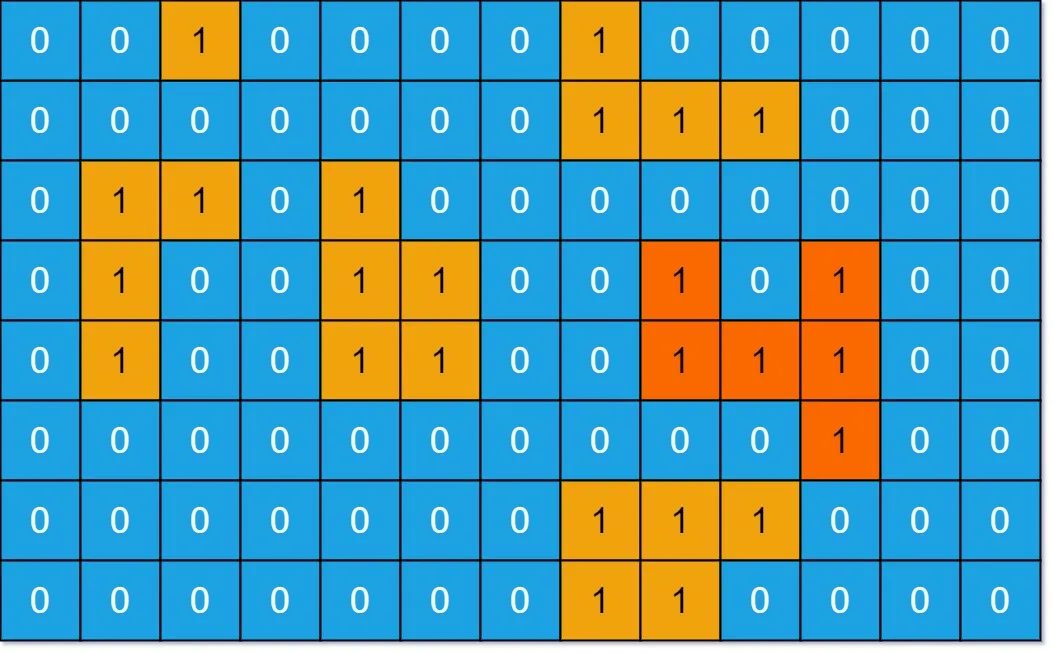：,,输入：grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]] 输出：6 解释：答案不应该是 11 ，因为岛屿只能包含水平或垂直这四个方向上的 1 。,给你一个大小为 m x n 的二进制矩阵 grid ，其中 0 表示一个海洋单元格、1 表示一个陆地单元格。,一次 移动 是指从一个陆地单元格走到另一个相邻（上、下、左、右）的陆地单元格或跨过 grid 的边界。,返回网格中 无法 在任意次数的移动中离开网格边界的陆地单元格的数量。,示例 1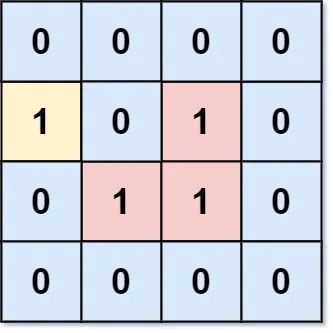：,,输入：grid = [[0,0,0,0],[1,0,1,0],[0,1,1,0],[0,0,0,0]] 输出：3 解释：有三个 1 被 0 包围。一个 1 没有被包围，因为它在边界上。,二维矩阵 grid 由 0 （土地）和 1 （水）组成。岛是由最大的4个方向连通的 0 组成的群，封闭岛是一个 完全 由1包围（左、上、右、下）的岛。,请返回 封闭岛屿 的数目。,示例 1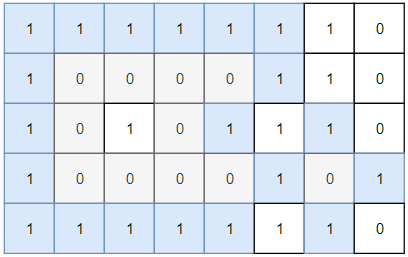：,,输入：grid = [[1,1,1,1,1,1,1,0],[1,0,0,0,0,1,1,0],[1,0,1,0,1,1,1,0],[1,0,0,0,0,1,0,1],[1,1,1,1,1,1,1,0]] 输出：2 解释： 灰色区域的岛屿是封闭岛屿，因为这座岛屿完全被水域包围（即被 1 区域包围）。,给你两个 m x n 的二进制矩阵 grid1 和 grid2 ，它们只包含 0 （表示水域）和 1 （表示陆地）。一个 岛屿 是由 四个方向 （水平或者竖直）上相邻的 1 组成的区域。任何矩阵以外的区域都视为水域。,如果 grid2 的一个岛屿，被 grid1 的一个岛屿 完全 包含，也就是说 grid2 中该岛屿的每一个格子都被 grid1 中同一个岛屿完全包含，那么我们称 grid2 中的这个岛屿为 子岛屿 。,请你返回 grid2 中 子岛屿 的 数目 。,示例 1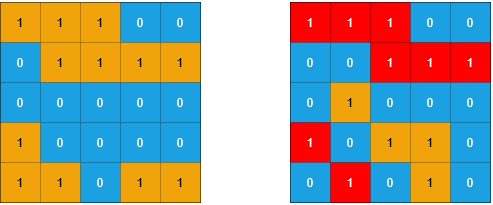：,,输入：grid1 = [[1,1,1,0,0],[0,1,1,1,1],[0,0,0,0,0],[1,0,0,0,0],[1,1,0,1,1]], grid2 = [[1,1,1,0,0],[0,0,1,1,1],[0,1,0,0,0],[1,0,1,1,0],[0,1,0,1,0]] 输出：3 解释：如上图所示，左边为 grid1 ，右边为 grid2 。 grid2 中标红的 1 区域是子岛屿，总共有 3 个子岛屿。