疯狂ios讲义疯狂连载之实现游戏逻辑（2）

13.6.5 定义获取通道的工具方法

这里所谓的通道指的是一个方块上、下、左、右4个方向上的空白方块图13.10显示了一个方块四周的通道。

图13.10 方块四周的通道

下面是获取某个坐标点四周通道的4个方法。

程序清单codes/13/Link/Link/sources/board/FKGameService.m

13.6.6 没有转折点的横向连接

如果两个FKPiece在FKPiece二维数组中的第二维索引值相等那么这两个FKPiece就位于同一行如前面的linkWithBeginPiece:endPiece:方法中①号代码所示此时程序需要调用isXBlockFromP1: toP2:pieceWidth:判断p1、p2之间是否有障碍。下面是该方法的代码。

程序清单codes/13/Link/Link/sources/board/FKGameService.m

从上面的判断可以看出如果两个方块位于同一行且它们之间没有障碍那么这两个方块就可以消除两个方块的连接信息就是它们的中心。

13.6.7 没有转折点的纵向连接

与之相似的是如果两个FKPiece在FKPiece二维数组中的第一维索引值相等那么这两个FKPiece就位于同一列如前面的linkWithBeginPiece:endPiece:方法中②号代码所示此时程序需要调用isYBlockFromP1: toP2:pieceHeight:方法判断p1、p2之间是否有障碍。下面是该方法的代码。

程序清单codes/13/Link/Link/sources/board/FKGameService.m

13.6.8 一个转折点的连接

对于两个方块的连接线上只有一个转折点的情况程序需要先找到这个转折点。为了找到这个转折点程序定义遍历两个通道并获取它们交点的一个方法。

程序清单codes/13/Link/Link/sources/board/FKGameService.m

为了找出两个方块连接线上的连接点程序同样需要分析p1、p2两个点的位置分布。根据前面的分析我们知道p2要么位于p1的右上角要么位于p1的右下角。

注意

对于p2位于p1的左上角和左下角的情况只要把p1、p2交换即可。

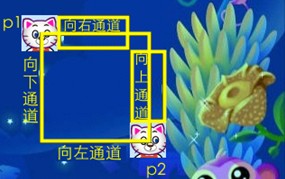
对于p2位于p1的右上角的情形如图13.11所示。

从图13.11可以看出当p2位于p1的右上角时应该计算p1的左通道与p2的向下通道是否有交点p1的向上通道与p2的向左通道是否有交点。

对于p2位于p1的右下角的情形如图13.12所示。

从图13.12可以看出当p2位于p1的右上角时应该计算p1的向右通道与p2的向上通道是否有交点p1的向下通道与p2的向左通道是否有交点。

图13.11p2位于p1的右上角

图13.12p2位于p1的右下角

考虑到p1与p2具有上面两种分布情形程序提供了如下方法进行处理。

程序清单codes/13/Link/Link/sources/board/FKGameService.m

上面的两行粗体字代码分别处理了p2位于p1的右上和右下的两种情形。

程序中用到了isLeftUp、isLeftDown、isRightUp、isRightDown方法来判断p2位于p1的左上、左下、右上、右下4种情形这4个方法的实现比较简单只要对它们的X、Y坐标进行简单判断即可代码如下。

程序清单codes/13/Link/Link/sources/board/FKGameService.m

——————本文节选自《疯狂ios讲义上》