近两年,“大力(算力)出奇迹”的大模型成为人工智能领域多数研究者的追求趋势。然而,其背后巨大的计算成本与资源耗费问题也弊端渐显,一部分科学家开始对大模型投以严肃的目光,并积极寻求解决之道。新的研究表明,要实现 AI 模型的优秀性能,并不一定要依靠堆算力与堆规模。
深度学习火热十年,不得不说,其机遇与瓶颈在这十年的研究与实践中已吸引了大量的目光与讨论。
其中,瓶颈维度,最引人注意的莫过于深度学习的黑盒子特性(缺乏可解释性)与“大力出奇迹”(模型参数越来越大,算力需求越来越大,计算成本也越来越高)。此外,还有模型的稳定性不足、安全漏洞等等问题。
而本质上,这些问题部分是由深度神经网络的“开环”系统性质所引起。要破除深度学习的 B 面“魔咒”,单靠扩大模型规模与堆算力或许远远不够,而是要追根溯源,从构成人工智能系统的基本原理,从一个新的视角(如闭环)理解“智能”。
7月12日,人工智能领域的三位知名华人科学家马毅、曹颖与沈向洋便联名在arXiv上发表了一篇文章,“On the Principles of Parsimony and Self-Consistency for the Emergence of Intelligence”,提出了一个理解深度网络的新框架:压缩闭环转录(compressive closed-loop transcription)。
这个框架包含两个原理:简约性(parsimony)与自洽性/自一致性(self-consistency),分别对应 AI 模型学习过程中的“学习什么”与“如何学习”,被认为是构成人工/自然智能的两大基础,在国内外的人工智能研究领域引起了广泛关注。

论文链接:
https://arxiv.org/pdf/2207.04630.pdf
三位科学家认为,真正的智能必须具备两个特征,一是可解释性,二是可计算性。
然而,在过去十年,人工智能的进步主要基于使用“蛮力”训练模型的深度学习方法,在这种情况下,虽然 AI 模型也能获得功能模块来进行感知与决策,但学习到的特征表示往往是隐式的,难以解释。
此外,单靠堆算力来训练模型,也使得 AI 模型的规模不断增大,计算成本不断增加,且在落地应用中出现了许多问题,如神经崩溃导致学习到的表征缺少多样性,模式崩溃导致训练缺乏稳定性,模型对适应性和对灾难性遗忘的敏感性不佳等等。
三位科学家认为,之所以出现上述问题,是因为当前的深度网络中,用于分类的判别模型和用于采样或重放的生成模型的训练在大部分情况下是分开的。此类模型通常是开环系统,需要通过监督或自监督进行端到端的训练。而维纳等人早就发现,这样的开环系统不能自动纠正预测中的错误,也不能适应环境的变化。
因此,他们主张在控制系统中引入“闭环反馈”,让系统能够学习自行纠正错误。在这次的研究中,他们也发现:用判别模型和生成模型组成一个完整的闭环系统,系统就可以自主学习(无需外部监督),并且更高效,稳定,适应性也强。


图注:左右到右分别为沈向洋(港中深校长讲席教授,美国国家工程院外籍院士,原微软全球执行副总裁)、曹颖(美国国家科学院院士,加州大学伯克利分校教授)与马毅(加州大学伯克利分校教授)。
智能的两个原理:简约性与自洽性
在这篇工作中,三位科学家提出了解释人工智能构成的两个基本原理,分别是简约性与自洽性(也称为“自一致性”),并以视觉图像数据建模为例,从简约性和自洽性的第一原理推导出了压缩闭环转录框架。
简约性
所谓简约性,就是“学习什么”。智能的简约性原理,要求系统通过计算有效的方式来获得紧凑和结构化的表示。也就是说,智能系统可以使用任何描述世界的结构化模型,只要它们能够简单有效地模拟现实感官数据中的有用结构。系统应该能够准确有效地评估学习模型的好坏,并且使用的衡量标准是基础、通用、易于计算和优化的。
以视觉数据建模为例,简约原理试图找到一个(非线性)变换 f 来实现以下目标:
压缩:将高维感官数据 x 映射到低维表示 z;
线性化:将分布在非线性子流形上的每一类对象映射到线性子空间;
划痕(scarification):将不同的类映射到具有独立或最大不连贯基础的子空间。
也就是将可能位于高维空间中的一系列低维子流形上的真实世界数据分别转换为独立的低维线性子空间系列。这种模型称为“线性判别表示”(linear discriminative representation,LDR),压缩过程如图 2 所示:
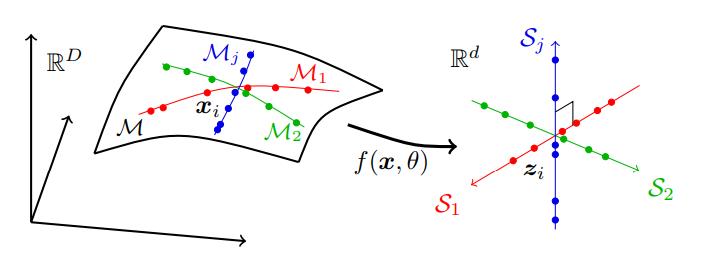
图 2:寻求线性和判别表示,将通常分布在许多非线性低维子流形上的高维感官数据映射到与子流形具有相同维度的独立线性子空间集。
在 LDR 模型系列中,存在衡量简约性的内在度量。也就是说,给定一个 LDR,我们可以计算所有子空间上的所有特征所跨越的总“体积”以及每个类别的特征所跨越的“体积”之和。然后,这两个体积之间的比率给出了一个自然的衡量标准,表明 LDR 模型有多好(往往越大越好)。
根据信息论,分布的体积可以通过其速率失真来衡量。
马毅团队在2022年的一个工作“ReduNet: A White-box Deep Network from the Principle of Maximizing Rate Reduction”表明,如果使用高斯的率失真函数并选择一个通用的深度网络(比如 ResNet)来对映射 f(x, θ) 进行建模,通过最大限度地降低编码率。

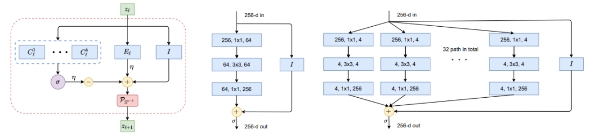
图 5:非线性映射 f 的构建块。图左:ReduNet 的一层,作为投影梯度上升的一次迭代,它精确地由扩展或压缩线性算子、非线性 softmax、跳过连接和归一化组成。图中和图右:分别是一层 ResNet 和 ResNeXt。
敏锐的读者可能已经认识到,这样的图表与 ResNet(图 5 中间)等流行的“久经考验”的深层网络非常相似,包括 ResNeXt 中的平行列(图 5 右)和专家混合(MoE)。
从展开优化方案的角度来看,这为一类深度神经网络提供了有力的解释。甚至在现代深度网络兴起之前,用于寻求稀疏性的迭代优化方案,例如 ISTA 或 FISTA 就已被解释为可学习的深度网络。
通过实验,他们证明,压缩可以诞生一种有建设性的方式来推导深度神经网络,包括它的架构和参数,作为一个完全可解释的白盒:它的层对促进简约的原理性目标进行迭代和增量优化。因此,对于如此获得的深度网络,ReduNets,从数据 X 作为输入开始,每一层的算子和参数都以完全向前展开的方式构造和初始化。
这与深度学习中的流行做法非常不同:从一个随机构建和初始化的网络开始,然后通过反向传播进行全局调整。人们普遍认为,由于需要对称突触和复杂的反馈形式,大脑不太可能利用反向传播作为其学习机制。在这里,前向展开优化只依赖于可以硬连线的相邻层之间的操作,因此更容易实现和利用。
一旦我们意识到深度网络本身的作用是进行(基于梯度的)迭代优化以压缩、线性化和稀疏化数据,那么就很容易理解过去十年人工神经网络的“进化”,尤其有助于解释为什么只有少数 AI 系统通过人工选择过程脱颖而出:从 MLP 到 CNN 到 ResNet 到 Transformer。
相比之下,网络结构的随机搜索,例如神经架构搜索,并没有产生能够有效执行一般任务的网络架构。他们猜想,成功的架构在模拟数据压缩的迭代优化方案方面变得越来越有效和灵活。前面提到的 ReduNet 和 ResNet/ResNeXt 之间的相似性可以例证。当然,还有许多其他例子。
自洽性
自洽性是关于“如何学习”,即自主智能系统通过最小化被观察者和再生者之间的内部差异来寻求最自洽的模型来观察外部世界。
仅凭借简约原理并不能确保学习模型能够捕获感知外部世界数据中的所有重要信息。
例如,通过最小化交叉熵将每个类映射到一维“one-hot”向量,可以被视为一种简约的形式。它可能会学习到一个好的分类器,但学习到的特征会崩溃为单例,称为“神经崩溃”。如此学习来的特征不包含足够的信息来重新生成原始数据。即使我们考虑更一般的 LDR 模型类别,单独的降速目标也不会自动确定环境特征空间的正确维度。如果特征空间维度太低,学习到的模型会欠拟合数据;如果太高,模型可能会过拟合。
在他们看来,感知的目标是学习一切可预测的感知内容。智能系统应该能够从压缩表示中重新生成观察到的数据的分布,生成后,无论它尽再大的努力,它自身也无法区分这个分布。
论文强调,自洽和简约这两个原理是高度互补的,应该始终一起使用。仅靠自洽不能确保压缩或效率方面的增益。
在数学和计算上,使用过度参数化的模型拟合任何训练数据或通过在具有相同维度的域之间建立一对一映射来确保一致性,而不需要学习数据分布中的内在结构是很容易的。只有通过压缩,智能系统才能被迫在高维感知数据中发现内在的低维结构,并以最紧凑的方式在特征空间中转换和表示这些结构,以便将来使用。
此外,只有通过压缩,我们才能容易地理解过度参数化的原因,比如,像 DNN 通常通过数百个通道进行特征提升,如果其纯粹目的是在高维特征空间中进行压缩,则不会导致过度拟合:提升有助于减少数据中的非线性,从而使其更容易压缩和线性化。后续层的作用是执行压缩(和线性化),通常层数越多,压缩效果越好。
在压缩到诸如 LDR 之类的结构化表示的特殊情况下,论文将一类自动编码(具体见原论文)称为“转录”(transcription)。这里的难点在于如何使目标在计算上易于处理,从而在物理上可以实现。
速率降低 ΔR 给出了退化分布之间的明确首要距离度量。但它仅适用于子空间或高斯的混合,而不适用于一般分布!而我们只能期望内部结构化表示 z 的分布是子空间或高斯的混合,而不是原始数据 x。
这导致了一个关于学习“自洽”表示的相当深刻的问题:为了验证外部世界的内部模型是否正确,自主系统真的需要测量数据空间中的差异吗?
答案是否定的。
关键是要意识到,要比较 x 和 x^,智能体只需要通过相同的映射 f 比较它们各自的内部特征 z = f(x) 和 z^ = f(x^),来使 z 紧凑和结构化。
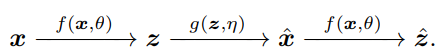
测量 z 空间中的分布差异实际上是定义明确且有效的:可以说,在自然智能中,学习内部测量差异是有独立自主系统的大脑唯一可以做的事情。
这有效地生成了一个“闭环”反馈系统,整个过程如图 6 所示。
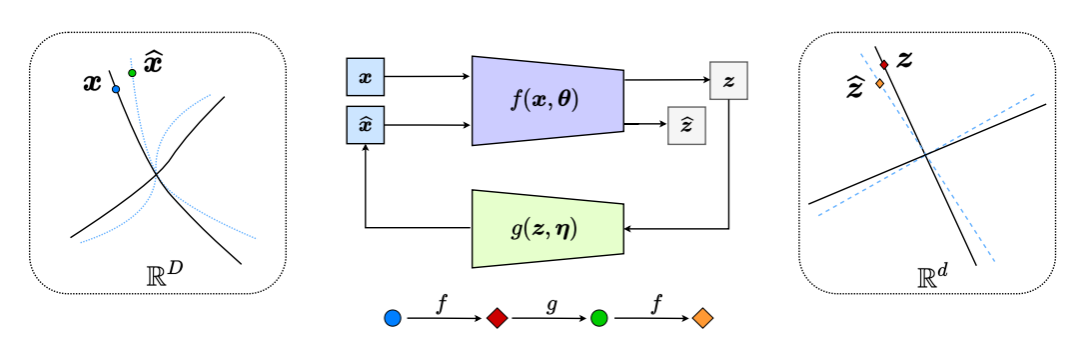
图 6:非线性数据子流形到 LDR 的压缩闭环转录(通过在内部比较和最小化 z 和 z^ 的差异)。这导致了编码器/传感器 f 和解码器/控制器 g 之间的自然追逃博弈,使解码的 x^(蓝色虚线)的分布追逐并匹配观察到的数据 x(黑色实线)的分布。
人们可以将单独学习 DNN 分类器 f 或生成器 g 的流行做法解释为学习闭环系统的开放式部分(图 6)。这种目前流行的做法与开环控制非常相似,控制领域早已知道它存在问题且成本高昂:训练这样的部分需要对期望的输出(如类标签)进行监督;如果数据分布、系统参数或任务发生变化,这种开环系统的部署本质上是缺少稳定性、鲁棒性或自适应性的。例如,在有监督的环境中训练的深度分类网络,如果重新训练来处理具有新数据类别的新任务,通常会出现灾难性的遗忘。
相比之下,闭环系统本质上更加稳定和自适应。事实上,Hinton 等人在1995年就已经提出了这一点。判别和生成部分需要分别作为完整学习过程的“唤醒”和“睡眠”阶段结合起来。
然而,仅仅闭环是不够的。
论文主张任何智能体都需要一种内部博弈机制,以便能够通过自我批评进行自我学习!这当中遵循的是博弈作为一种普遍有效的学习方式的概念:反复应用当前模型或策略来对抗对抗性批评,从而根据通过闭环收到的反馈不断改进模型或策略!
在这样的框架内,编码器 f 承担双重角色:除了通过最大化速率降低 ΔR(Z) 来学习数据 x 的表示 z(如 2.1 节中所做的那样),它还应该作为反馈“传感器”,主动检测数据 x 和生成的 x^ 之间的差异。解码器 g 也承担双重角色:它是控制器,与 f 所检测到的 x 和 xˆ 之间的差异联系起来;同时又是解码器,尝试将整体的编码率最小化来实现目标(让步于给定的准确度)。
因此,最优的“简约”和“自洽”表示元组 (z, f, g) 可以解释为 f(θ) 和 g(η) 之间的零和博弈的平衡点,而不是基于组合速率降低的效用:
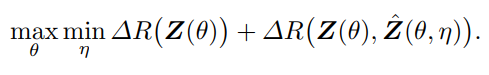
以上讨论是两个原理在有监督情况下的表现。
但论文强调,他们所提出的压缩闭环转录框架能够通过自我监督和自我批评来进行自我学习!
此外,由于速率降低已经为学习结构找到显式(子空间类型)表示,使得过去的知识在学习新任务/数据时更容易保留,可以作为保持自一致性的先验(记忆) 。
最近的实证研究表明,这可以产生第一个具有固定内存的自包含神经系统,可以在不遭受灾难性遗忘的情况下逐步学习良好的 LDR 表示。对于这样一个闭环系统,遗忘(如果有的话)是相当优雅的。
此外,当再次将旧类别的图像提供给系统进行审查时,可以进一步巩固学习到的表示——这一特征与人类记忆的特征非常相似。从某种意义上说,这种受约束的闭环公式基本上确保了视觉记忆的形成可以是贝叶斯和自适应的——假设这些特征对大脑来说是理想的话。
如图 8 所示,如此学习的自动编码不仅表现出良好的样本一致性,而且学习到的特征还表现出清晰且有意义的局部低维(薄)结构。

图 8:图左:在 CIFAR-10 数据集(有 10 个类别的 50,000 张图像)的无监督设置中学习的自动编码的 x 与相应解码的 x^ 之间的比较。图右:10 个类别的无监督学习特征的 t-SNE,以及几个邻域及其相关图像的可视化。注意可视化特征中的局部薄(接近一维)结构,从数百维的特征空间投影。
更令人惊讶的是,即使在训练期间没有提供任何类信息,子空间或特征相关的块对角结构也开始出现在为类学习的特征中(图 9)!因此,所学特征的结构类似于在灵长类动物大脑中观察到的类别选择区域。
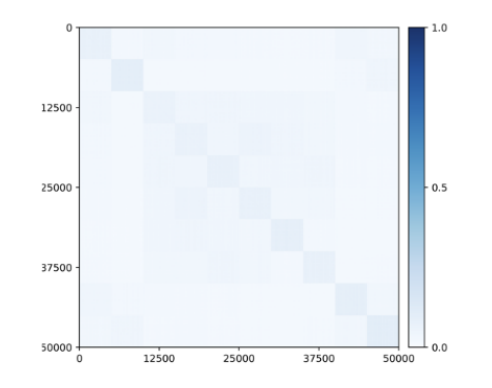
图 9:通过闭环转录,属于 10 个类别 (CIFAR-10) 的 50,000 张图像的无监督学习特征之间的相关性。与类一致的块对角结构在没有任何监督的情况下出现。
通用学习引擎:3D 视觉与图形结合
论文总结,简约性和自洽性揭示了深度网络的角色是成为外部观察和内部表征之间非线性映射的模型。
此外,论文强调,闭环压缩结构在自然界中无处不在,适用于所有智能生物,这一点可以见于大脑(压缩感觉信息)、脊髓回路(压缩肌肉运动)、DNA(压缩蛋白质的功能信息)等等生物示例。因此,他们认为, 压缩闭环转录可能是所有智能行为背后的通用学习引擎。它使智能生物和系统能够从看似复杂和无组织的输入中发现和提炼低维结构,并将它们转换为紧凑和有组织的内部结构,以便记忆和利用。
为了说明这个框架的通用性,论文研究了另外两个任务:3D 感知和决策(LeCun 认为这是自主智能系统的两个关键模块)。本文整理,仅介绍 3D 感知中计算机视觉与计算机图形学的闭环。
David Marr 在其颇具影响力的著作《视觉》一书中提出的 3D 视觉经典范式提倡“分而治之”的方法,将 3D 感知任务划分为几个模块化过程:从低级 2D 处理(如边缘检测、轮廓草图)、中级 2.5D 解析(如分组、分割、图形和地面),以及高级 3D 重建(如姿势、形状)和识别(如对象),而相反,压缩闭环转录框架提倡“联合构建”思想。
感知是压缩闭环转录?更准确地说,世界上物体的形状、外观甚至动态的 3D 表示应该是我们的大脑内部开发的最紧凑和结构化的表示,以相应地解释所有感知到的视觉观察。如果是这样,那么这两个原理表明紧凑和结构化的 3D 表示就是要寻找的内部模型。这意味着我们可以并且应该在一个闭环计算框架内统一计算机视觉和计算机图形,如下图所示:
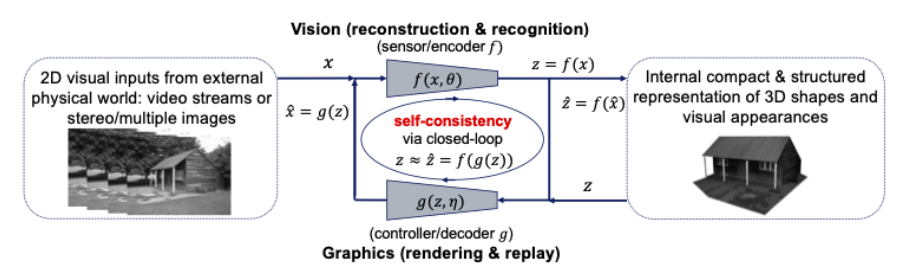
图10:计算机视觉和图形之间的闭环关系,用于视觉输入的紧凑和结构化 3D 模型
计算机视觉通常被解释为为所有 2D 视觉输入重建和识别内部 3D 模型的前向过程,而计算机图形学表示其对内部 3D 模型进行渲染和动画处理的逆过程。将这两个过程直接组合成一个闭环系统可能会带来巨大的计算和实践好处:几何形状、视觉外观和动力学中的所有丰富结构(例如稀疏性和平滑度)可以一起用于统一的 3D 模型, 最紧凑,且与所有视觉输入一致。
计算机视觉中的识别技术可以帮助计算机图形学在形状和外观空间中构建紧凑模型,并为创建逼真的 3D 内容提供新的方法。另一方面,计算机图形学中的 3D 建模和仿真技术可以预测、学习和验证计算机视觉算法分析的真实对象和场景的属性和行为。视觉和图形社区长期以来一直在实践“综合分析”的方法。
外观和形状的统一表示?基于图像的渲染,其中,通过从一组给定图像中学习来生成新视图,可以被视为早期尝试用简约和自洽的原理缩小视觉和图形之间的差距。特别是,全光采样表明,可以用所需的最少图像数量(简约性)来实现抗锯齿图像(自洽性)。
更广泛的智能
智能的神经科学
人们会期望基本的智能原理对大脑的设计产生重大影响。简约和自洽原理为灵长类视觉系统的几个实验观察提供了新的思路。更重要的是,它们揭示了未来实验中要寻找的目标。
作者团队已经证明,仅寻求内部简约和预测性表示就足以实现“自监督”,允许结构自动出现在通过压缩闭环转录学习的最终表示中。
例如,图 9 显示无监督数据转录学习自动区分不同类别的特征,为在大脑中观察到的类别选择性表示提供了解释。这些特征也为灵长类大脑中稀疏编码和子空间编码的广泛观察提供了合理的解释。此外,除了视觉数据建模,最近的神经科学研究表明,大脑中出现的其他结构化表示(例如“位置细胞”)也可能是以最压缩的方式编码空间信息的结果。
可以说,最大编码率降低 (MCR2) 原理在精神上类似于认知科学中的“自由能最小化原理”(free energy minimization principle),后者试图通过能量最小化为贝叶斯推理提供框架。但与自由能的一般概念不同,速率降低在计算上易于处理且可直接优化,因为它可以以封闭的形式表示。此外,这两个原理的相互作用表明,正确模型(类)的自主学习应该通过对这种效用的闭环最大化博弈来完成,而不是单独进行最小化。因此,他们相信,压缩闭环转录框架为如何实际实施贝叶斯推理提供了一个新的视角。
这个框架也被他们认为阐明了大脑使用的整体学习架构,可以通过展开优化方案来构建前馈段,且不需要通过反向传播从随机网络中学习。此外,框架存在一个互补的生成部分,可以形成一个闭环反馈系统来指导学习。
最后,框架揭示了许多对“预测编码”大脑机制感兴趣的神经科学家所寻求的难以捉摸的“预测错误”信号,这是一种与压缩闭环转录产生共振的计算方案:为了让计算更容易,应在表示的最后阶段测量传入和生成的观测值之间的差异。
迈向更高层次的智能
马毅等人的工作认为,压缩闭环转录与Hinton等人在1995年提出的框架相比,在计算上更易于处理和可扩展。而且,循环的学习非线性编码/解码映射(通常表现为深度网络),本质上在外部无组织的原始感官数据(如视觉、听觉等)和内部紧凑和结构化表示之间提供了一个重要的“接口”。
不过,他们也指出,这两个原理并不一定能解释智能的所有方面。高级语义、符号或逻辑推理的出现和发展背后的计算机制仍然难以捉摸。直到今天,关于这种高级符号智能是可以从持续学习中产生还是必须进行硬编码,仍然存在争议。
在三位科学家看来,诸如子空间之类的结构化内部表示是高级语义或符号概念出现的必要中间步骤——每个子空间对应一个离散的(对象)类别。如此抽象的离散概念之间的其他统计、因果或逻辑关系可以进一步简化建模为紧凑和结构化(比如稀疏)图,每个节点代表一个子空间/类别。可以通过自动编码来学习图形以确保自一致性。
他们推测,只有在个体智能体学习的紧凑和结构化表示之上,高级智能(具有可共享的符号知识)的出现和发展才有可能。因此,他们建议,应该通过智能系统之间有效的信息交流或知识迁移来探索高级智能出现的新原理(如果高级智能存在的话)。
此外,更高级别的智能应该与我们在本文中提出的两个原理有两个共同点:
- 可解释性:所有原理都应该有助于将智能的计算机制揭示为白盒,包括可测量的目标、相关的计算架构和学习表示的结构。
- 可计算性:任何新的智能原理都必须在计算上易于处理和可扩展,可以通过计算机或自然物理实现,并最终得到科学证据的证实。
只有具备可解释和可计算性,我们才能无需依赖当前昂贵且耗时的“试错”方法来推进人工智能的进步,能够描述完成这些任务所需的最少数据和计算资源,而不是简单地提倡“越大越好”的蛮力方法。智慧不应该是最足智多谋的人的特权,在一套正确的原则下,任何人都应该能够设计和构建下一代智能系统,无论大小,其自主性、能力和效率最终都可以模仿甚至超过动物和人类。
论文链接:
https://arxiv.org/pdf/2207.04630.pdf