基于对抗梯度的探索模型及其在点击预估中的应用

1. 摘要

排序模型在广告、推荐和搜索系统中起到了至关重要的作用。在排序模块中，点击率预估技术又是重中之重。目前工业界的点击率预估技术大多采用深度学习算法，基于数据驱动来训练深度神经网络，然而数据驱动带来的相应问题是推荐系统中的新进项目会存在冷启动问题。

探索与利用（Exploration-Exploitation，E&E）方法通常用于处理大规模在线推荐系统中的数据循环问题。过去的研究通常认为模型预估不确定度高意味着潜在收益也较高，因此大部分研究文献聚焦到对不确定度的估计上。对于采用流式训练的在线推荐系统而言，探索策略会对训练样本的收集产生较大影响，进而影响模型的进一步学习。然而，当前大多数探索策略并不能很好的建模被探索的样本如何对后续模型学习产生影响。因此，我们设计了一个拟探索（Pseudo-Exploration） 模块来模拟样本被成功探索并展现后对推荐模型后续学习的影响。

拟探索过程通过在模型输入中添加对抗扰动来实现，我们同时也给出了该过程相应的理论分析以及证明。基于此，我们将该方法命名为基于对抗梯度的探索策略（ A dversarial G radient driven E xploration，以下简称 AGE ）。为了提高探索的效率，我们还提出了一个动态门控单元用来过滤低价值样本，避免将资源浪费在低价值的探索上。为了验证AGE算法的有效性，我们不仅在公开学术数据集上进行了大量的实验，也将AGE模型部署到了阿里妈妈展示广告平台上并取得了良好的线上收益。该工作已被KDD 2022 Research Track收录为Full Paper，欢迎阅读交流。

论文： Adversarial Gradient Driven Exploration for Deep Click-Through Rate Prediction

下载： https://arxiv.org/abs/2112.11136

2. 背景

在广告系统中，点击率（CTR）预估模型通常采用流式方式加以训练，而流式数据的来源又是由部署在线上的CTR模型产出，这就产生了所谓的 数据循环 问题。冷启动与长尾广告由于没有充分展现，CTR模型缺乏对这部分广告的训练数据，这也导致模型对这部分广告的估计可能存在较大误差，会使得这些广告更加难以展现，进而难以完成冷启动过程。具体而言，图一给出了广告真实点击率与展现数量之间的关系：我们系统中，一个新广告的展现平均需要达到约一万次，其点击率才能达到收敛态。这给许多在线系统带来了一个常见的难题，即如何在保证用户体验的前提下，为这些广告做好冷启动。

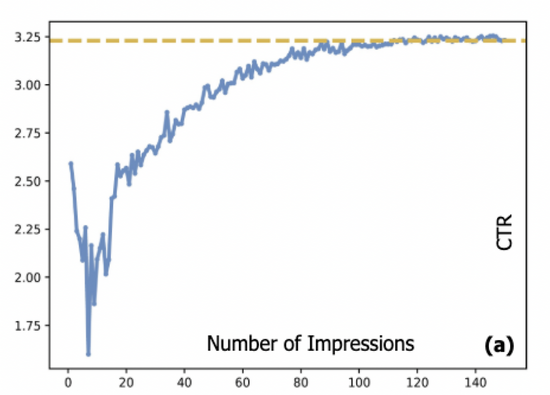
图一：广告CTR和展现次数之间的关系

探索和利用（E&E）算法通常被用来解决上述问题。在推荐或广告系统中，常见的方法（如Contextual Multi-Armed Bandits，上下文多臂老虎机）一般会将该问题按照如下方式加以建模。在每步中，系统会基于策略P选择一个操作（即为用户推荐一个项目_ _）。为了最大化累积奖励（通常使用总点击量来衡量），系统需要权衡当前是偏重探索，还是偏重利用。先前的研究通常认为，高不确定性是潜在回报的衡量指标。一方面，策略P需要优先选择当前效用较大的项目以最大化本轮收益；另一方面，算法也需要选择不确定度较大的操作以实现探索。如果用来表示权衡探索和利用的策略，那么系统对项目最终打分可以用如下公式表示：

不确定性估计已成为许多E&E算法的核心模块。不确定性可能源于数据的可变性、测量噪声和模型不稳定性（例如：参数的随机性），典型的估计方法包括蒙特卡洛MC-Dropout、贝叶斯神经网络、预测不确定性的高斯过程，以及基于梯度范数（模型权重）的不确定性建模等。在此基础上，有两种典型的探索策略：基于UCB的方法通常采用潜在回报的上限作为最终打分[1,2]，而基于汤普森采样的方法是通过从估计的概率分布中抽样来完成 [3]。

3. 方法介绍

我们认为，上述方法并未考虑一个完整的探索闭环。对于数据驱动的在线系统而言，探索的最终收益来自于从探索过程中获取的反馈数据，以及反馈数据对于模型的训练与更新。而模型预估的不确定度本身并不能完全反映整个反馈闭环。为此，我们引入了一个拟探索模块，用于模拟完成探索动作后反馈数据对于模型的影响，并以此来衡量探索的有效性。分析发现，探索的有效性不仅取决于模型的预估不确定度，还取决于“对抗扰动”的大小。所谓对抗扰动，指的是在模型的输入上加入的固定模长的扰动中使得模型输出变化最大的扰动向量。在论文中，我们也证明了，模型利用被探索的数据进行一次训练后，模型输出变化的期望等价于在输入向量中加入模长为不确定度、扰动向量为对抗梯度的增量向量。我们验证了按照这种方式进行建模，可以闭环地估计出被探索样本对模型的后续影响，从而估计出被探索样本的真实价值。

我们将这种方法称为 基于对抗梯度的探索（Adversarial Gradient driven Exploration） ，简称AGE。AGE模型由拟探索模块（Pseudo-Exploration Module）与动态门控阈值单元（Dynamic Gating Unit）两部分组成，其整体结构如图二所示。

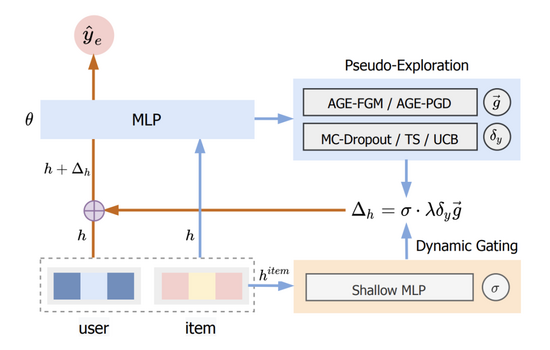
图二：AGE结构图

其中部分的详细介绍详见3.1节，部分的详见3.3节。

3.1 拟探索模块（Pseudo-Exploration Module）

3.1.1 模块简介

拟探索模块的主要目的是定量模拟模型使用探索样本加以训练后，对该样本打分的变化，从而估计探索对于模型的闭环影响。经过推导，我们发现可以通过公式(2)来完成上述过程，其中代表了探索后模型对该样本的打分，我们将其用于最终的排序。

上式表示我们不需要对原有模型参数进行任何操作，只需要在输入的表征中加上对抗梯度，预估不确定度以及手工设定的超参数的乘积，即可完成对探索后模型预估分的模拟。 其中参数 与 的计算方法，我们在下一节中介绍。本节后续我们将介绍拟探索模块中公式(2)的详细推导过程。

3.1.2 详细推导

对于每条数据样本而言，模型的训练将会影响两部分参数：该样本对应的表征（包含商品、用户embedding等）与模型参数。因为模型参数在训练中的目标是适应所有样本而不是单条样本，所以我们可以认为训练单条样本主要会对样本对应的表征产生影响，而模型参数本身只需要微小的调整。因此，在后续研究中，我们将忽略的调整，而仅关注样本对应的表征的变化。假设包含表征的样本真实label为，训练时，我们需要寻找到的更新量，以最小化损失函数。基于此，我们定义：

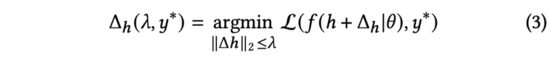
其中代表训练中使用的损失函数，而在CTR预估任务中一般使用交叉熵损失函数。同时，我们用来约束表征的最大变化。为了简化书写，后续我们将上述公式右侧写为。

依据拉格朗日中值定理，在的二范数接近0的情况下，我们可以将上述损失函数公式(3)推导为：

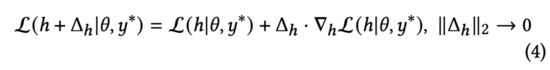
我们观察公式(4)，易发现该损失函数在与两个向量有相反的方向时，获得最小值。在公式(3)中，我们约束对抗扰动。因此，通过求解公式(3)，我们得到：

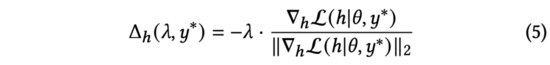
实践中，我们用来替代公式(5)中的归一化梯度。通过求导链式法则，可以展开为和两部分。进一步计算，得到：

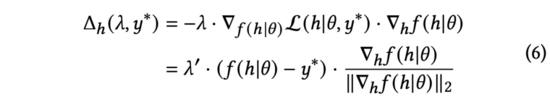
在上式中，我们将重新缩放到以保持等式的成立。尽管含义不同，但它们都是手动调节的超参数，故我们可以直接以完成替换。我们进一步简化公式(6)为：

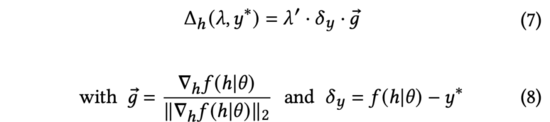
上式中，归一化梯度表示模型输出相对于输入表征的导数方向。由于真实的用户反馈在探索时无法得到，我们将使用预估不确定度来衡量预测得分与真实用户反馈之间的差值。

公式(7)中，我们找到了在的约束下可以最大化改变模型预测输出的解析解（推导与公式(3)到公式(5)相同）。进一步，我们也发现上述对输入表征添加的过程与对抗扰动（见公式(9)）的形式相同。

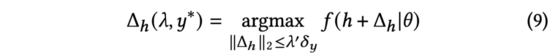
因此，我们利用对抗梯度来的替代公式(7)中的，并将我们的方法命名为基于对抗性梯度的探索算法。

公式(9)表明，AGE最有效的探索方式为给表征输入加入对抗扰动，以扰动后模型的输出结果为排序因子：以对抗梯度为输入表征的扰动向量方向，以及以预测不确定性度的扰动力度。于是，在得到和后，我们可以用下述公式来计算探索后的模型预测分数，该公式即为前述公式(2)。

3.2 实现细节

在AGE中，我们采用MC-Dropout的方法估计不确定度。具体说来，MC-Dropout为深度模型中的每个神经元赋予随机Mask权重，具体做法如下公式(11)所示。该方法的一个好处是，我们可以在不改变模型原始结构的基础上直接获取不确定性。在实际操作中，可以通过UCB的思想计算dropout的方差来表示不确定度，或者参考汤普森随机采样的方式通过计算采样与均值的差异来计算不确定度，也即公式（12）和公式（13）。

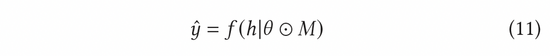
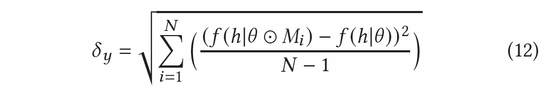
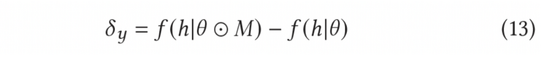
归一化对抗梯度可以根据公式(8)中的快速梯度法（FGM）来计算获得。为了更加精确地计算出对抗梯度，我们还可以进一步利用近端梯度下降（PGD）方法，多步迭代更新梯度，如公式（14）所示。

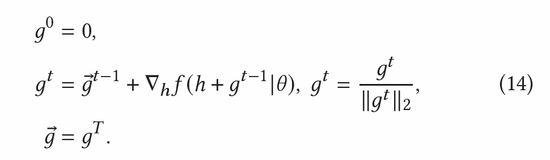
3.3 动态门控阈值单元（Dynamic Gating Unit）

在实践中，我们发现并非所有广告都值得探索。在一般的Top-K广告系统中，能够为最终用户展现的广告数量是相对较少。因此，本身点击率低的广告（比如广告本身质量较低），即使模型对这部分广告的预估存在很高的不确定性，但考虑广告系统的业务属性，其探索价值仍然是很低的。虽然我们可以通过探索获得了这些广告的大量数据，使得这些广告被模型充分训练而估计的更加准确；但因为这些广告的本身过低的点击率会使得即使充分探索后，这些广告依然无法自行获取流量，这样的探索无疑是低效的。在本文中，我们尝试了一种简单的启发式方法来提高探索的效率——如果模型对该广告的预估分数高于该广告在所有人群中的平均点击率，我们将进行探索；否则，探索将不会发生。

为了计算广告的平均点击率，我们引入了动态门控阈值单元（DGU）模块。DGU仅使用广告侧特征作为输入来预估广告的平均点击率。当模型的预估点击率低于DGU模块预估的广告平均点击率时，不予探索，反之则进行正常的探索。该过程如下式所示：

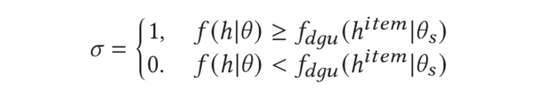
最终，我们将代入公式(10)中，获得如下AGE探索模型最终完整的计算方式。

4. 实验评测

4.1 离线实验

我们对比了三大类基线方法，包括基于随机采样的探索方法，基于深度模型的探索方法，以及基于梯度的探索方法，结果如表1所示。观察可得，基于汤普森采样（TS）方法构建的基线模型均优于基于UCB的模型，证明TS是一种更好的衡量模型不确定度的算法。此外，我们可以观察到AGE算法优于所有的基线方法，这也证明了AGE方法的有效性。具体而言，AGE-TS和AGE-UCB的表现均优于最好基线UR-gradient-TS和UR-gradient-UCB [4]，提升数值分别为5.41%和15.3%。而AGE-TS方法相比于不进行探索的基准方法提高了整整28.0%的点击量。值得注意的是，基于AGE的UCB和TS算法AGE-UCB和AGE-TS取得了相似的效果，基于gradient的UCB和TS算法并非如此，这也证明了AGE可以弥补UCB方法的不稳定性。

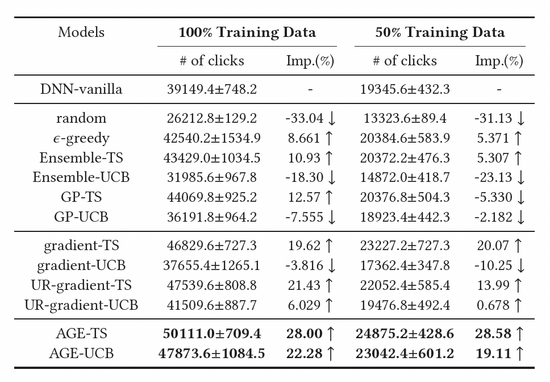
表1：离线实验结果

我们也进行了大量的消融实验来证明了各个模块的有效性。如表2所示，阈值单元、对抗梯度、不确定度单元，三者均不可或缺。为了进一步确定DGU的效果，我们尝试了不同的固定阈值参数，最后也发现其效果也不及DGU的动态阈值。

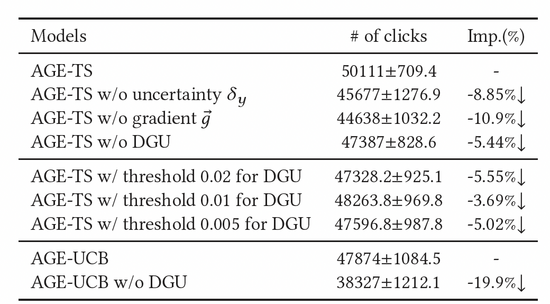
表2：消融实验结果

4.2 在线实验

我们也将AGE模型部署到阿里妈妈展示广告系统中，为了准确评估模型的探索价值，我们设计了基于公平桶的评测方法。如图三所示，我们首先设置桶C和桶D用于收集数据。在桶D中，我们部署AGE等探索算法，而在桶C中，我们采用不做探索的常规CTR模型。经过一段时间之后，我们将桶C和桶D获取的反馈数据分别应用于公平桶A和B上部署模型的训练。最终，我们将比较公平桶A和B上的模型效果。在线实验中，我们使用几个标准指标进行评估，包括点击率CTR、被探索广告的展现数量PV和预测CTR与真实CTR之比PCOC。此外，我们还引入了一个用于衡量广告主的满意度的业务指标（AFR）。

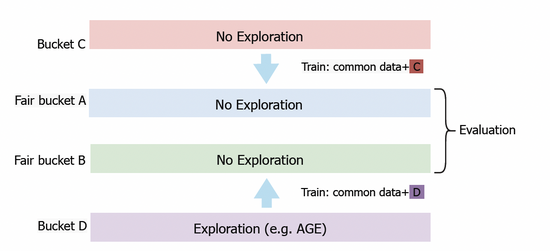
图三：公平桶实验方案

如表3所示，上述指标都得到了有效的提升。其中，AGE明显优于所有其他方法：CTR和PV分别比基线模型高6.4%和3.0%。同时AGE模型的使用还提升了模型的预测精度，即预估准度PCOC更接近1。更重要的是，AFR指标也有5.5%的提升，这表明我们的探索方法可以有效提升广告主的体验。

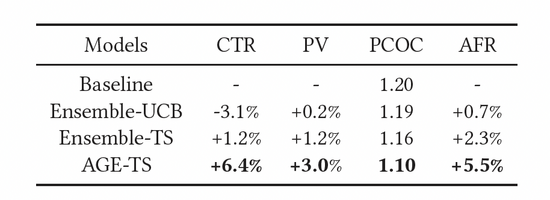
表3：在线实验结果

5. 总结

与大多数专注于估计潜在回报的探索&利用方法不同，我们的方法AGE从在线学习的数据驱动的角度重新构建了这一问题。除了可以估计当前模型预测的不确定度外，AGE算法借助拟探索模块，更进一步地考虑探索样本对模型训练的后续影响。我们在学术研究数据集和生产链路上都进行了A/B测试实验，相关结果均证实了AGE方法的有效性。今后我们会将AGE部署于更多的应用场景中。