如何在因果推断中更好地利用数据？

导读：本次分享题目为《如何在因果推断中更好地利用数据？》，主要介绍团队近期在因果上已发表论文的相关工作。本报告从两个方面来介绍我们如何利用更多的数据来做好因果推断，一个是利用历史对照数据来显式缓解混淆偏差，另一个是多源数据融合下的因果推断。

全文目录：

• 因果推断背景
• 纠偏因果树 GBCT
• 因果数据融合
• 在蚂蚁的业务应用

一、因果推断背景

常见的机器学习预测问题一般设置在同样的系统里面，如通常会假设独立同分布，比如预测吸烟的人中得肺癌的概率、图片分类等预测问题。而因果的问题则关心的是数据背后的机制，常见的问题如“吸烟是否导致肺癌”，类似的问题则为因果的问题。

在因果效应估计问题里有两类很重要的数据：一类是观测数据，另一类则为随机对照实验产生的实验数据。

• 观测数据是我们实际生活或产品积累下来的数据。比如抽烟的数据，有的人喜欢抽烟，观察数据则是抽烟者的相关数据，最终抽烟者中的一部分人得癌症。机器学习预测问题就是估计条件概率P（得肺癌｜吸烟），即给定吸烟的条件下，观察吸烟者得肺癌的概率。在上述的观测数据中，抽烟的分配实际上并不是随机的：每个人抽烟的偏好不同，同时也会受环境的影响。
• 回答因果问题最好的方式是进行随机对照实验。实验数据是通过随机对照的实验得到的。在随机对照实验中，treatment 的分配是随机的。假设需要通过做实验的方式得到“吸烟是否会导致肺癌”的结论，首先需要找到足够多的人，强制其中一半人抽烟，同时强制另一半人不抽烟，并观察两组人得肺癌的概率。虽然随机对照试验在部分场景下受制于道德、政策等因素而不可实现，在部分领域中随机对照实验仍可进行，比如在搜推广中的 A/B test 等。

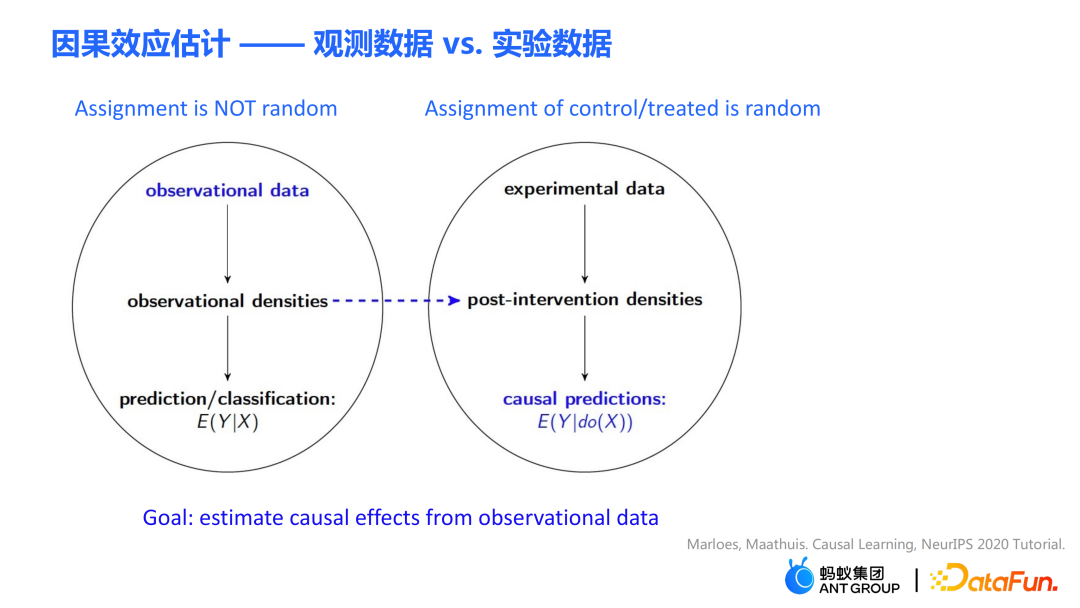
因果估计问题 E(Y|do(X)) 问题和传统的预测或分类问题 E(Y|X) 之间的主要区别在于：给定的条件中出现了 Judy Pearl 提出的干预表示符号 do。通过干预，强制将 X 变量设置为某个值。本次报告分享中的因果效应估计主要指的是从观测数据中估计因果效应。

在因果推断中如何更好地利用数据？本次报告将以两个团队近期已发表论文为例子去介绍这样一个话题。

• 第一个工作是如何更好地利用历史对照数据。比如在某个时间点举行了一个营销大促的活动，在这个时间点之前的时间称为“干预前”，在这个时间点之后的时间称为“干预后”。我们希望在干预前就知道采取干预将带来多少实际的效果，进而辅助我们做下一步决策。在这次营销活动开始之前，我们拥有用户的历史表现数据，第一个工作主要就是介绍如何利用好“干预前”的数据，辅助数据纠偏工作以更好地评估干预的效果。
• 第二个工作主要是介绍如何更好地利用多源异构数据。机器学习中也经常会涉及此类问题，常见的问题如 domain adaptation、transfer learning 等。在今天的报告中，将从因果的视角去考虑多源异构数据的利用问题，即假设在有多个数据源的情况下，如何更好地估计因果效应。

二、纠偏因果树 GBCT

1、传统的因果树

树算法主要由两个模块组成：

• 分裂准则：根据分裂准则将一个节点分裂成两个子节点
• 参数估计：分裂完成后，比如最终停止分裂，根据参数估计的方法在叶子节点上预测新样本或群体的因果效应

一些传统因果树算法是根据因果效应的异质性进行分裂的，基本思想是希望分裂之后的左子节点和右子节点的因果效应差异较大，通过分裂捕捉到不同数据分布的因果效应异质性。

传统因果树的分裂准则，比如：

• uplift tree 的分裂准则为最大化左右子节点的因果效应差异，差异的度量使用欧氏距离、KL 散度等距离度量；
• causal tree 分裂准则可直观地解释为最大化因果效应的平方。可通过数学证明，该分裂准则等价于最大化叶子节点因果效应方差。

常见的参数估计做法是直接在分裂后的叶子节点上将实验组的平均 outcome 减去对照组的平均 outcome，以此作为因果效应的估计值。如果是随机对照实验，则 treatment 的分配机制是随机的，由此计算得到的平均差值即为因果效应。随机分配机制保证实验组和对照组的数据分布是相同的，即称之为同质。

因果树中分裂得到子节点，可以保证分裂得到的左子节点和右子节点的分布是同质的吗？

2、纠偏因果树 GBCT

传统的 causal tree、uplift tree 并不能保证分裂后的左子节点和右子节点的分布是同质的。因此上一节提到的传统估计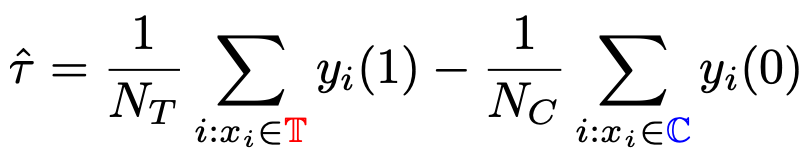是有偏的。

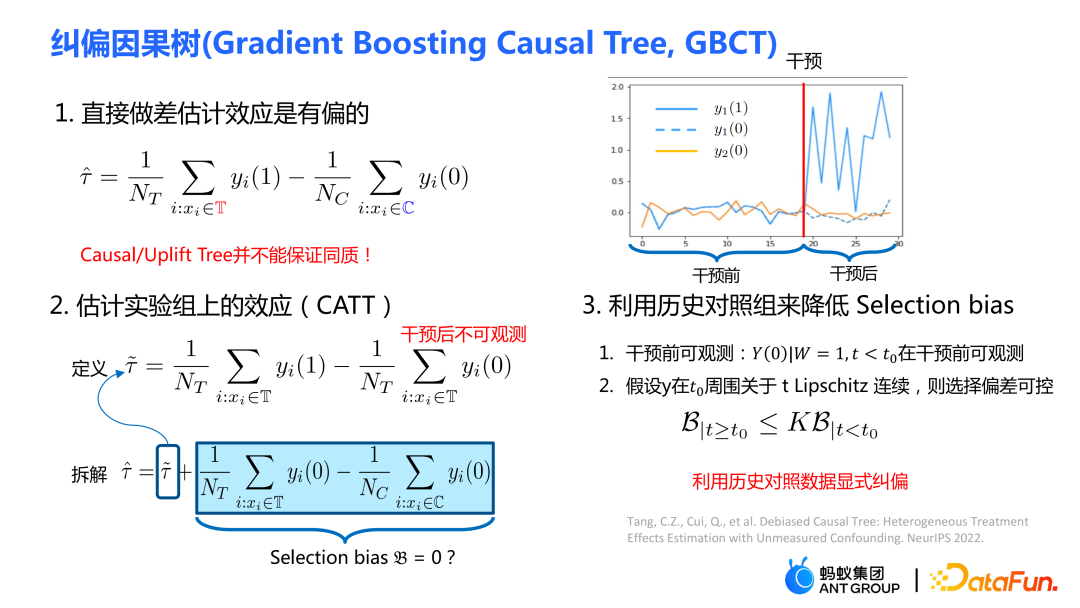
我们的工作关注于去估计实验组（treatment组）上的平均因果效应 CATT。CATT 的定义为：

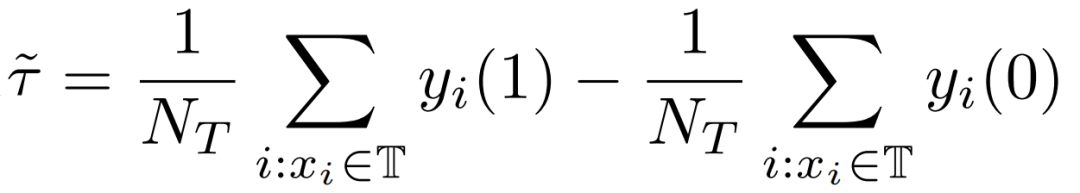
进一步，可将传统的因果效应估计拆分成两部分：

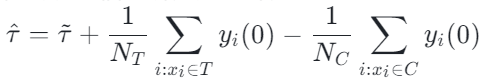
选择偏倚（selection bias/confounding bias）可定义为：

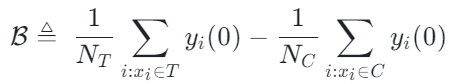
其直观含义为在实验组中 treatment=0 时的估计值，减去在对照组中 treatment=0 时的估计值。在传统的因果树中上述的 bias 是没有被刻画的，选择偏倚可能会影响我们的估计，从而导致最终的估计是有偏的。

我们的思路是利用产品或平台上积累的历史对照数据，从而显式地减少选择偏倚。具体操作是基于两个假设：

• 假设1：可观测到干预之前实验组和对照组在 treatment=0 的状态下的 outcome 的表现。以金融信贷产品中信用卡产品提额操作为例，在提额之前，我们可观察到用户平时的使用表现，即实验组和对照组在不提额状态下（treatment=0）的 outcome 的表现是可获得的；
• 假设2：假设 outcome 的 y 在干预前后满足一定的连续性。直观理解为一个用户或群体行为的变化在干预前后不会太剧烈。

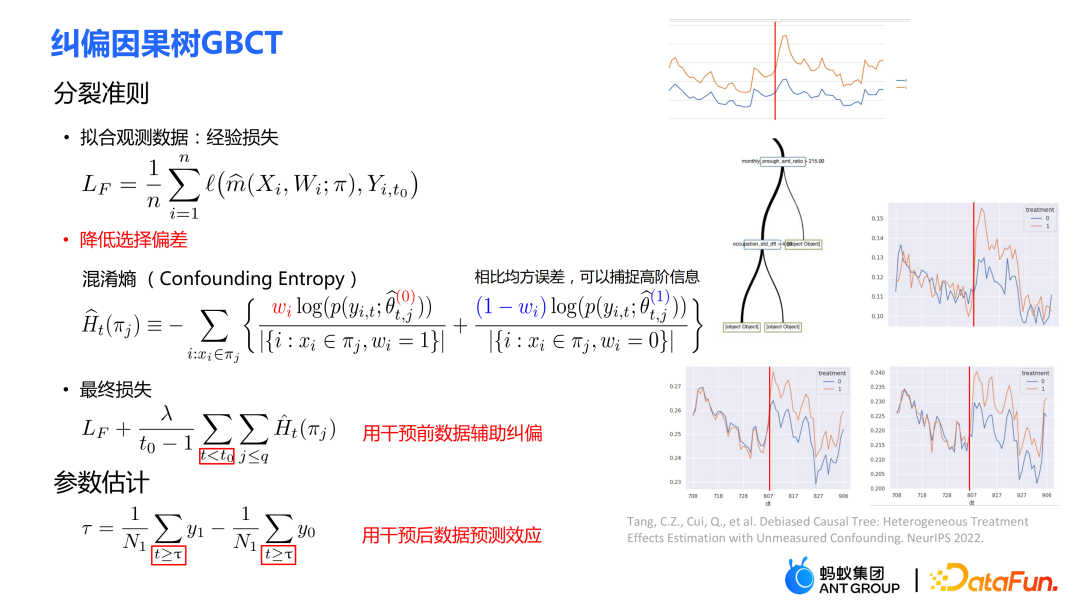
具体的做法：

① 分裂准则

• 分裂准则的第一部分与传统因果树类似，通过拟合历史数据的 outcome 从而降低经验损失。比如在不提额状态下通过函数拟合用户行为。
• 分裂准则的第二部分是使用混淆熵。混淆熵相对于均方误差而言，可以捕捉高阶信息。公式：

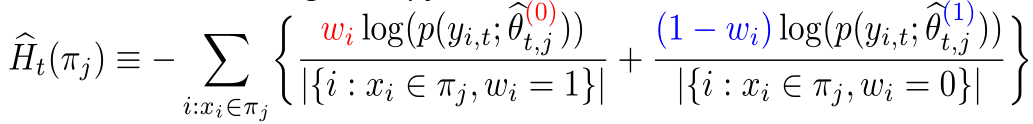
的直观含义是：在实验组中，使用对照组的模型进行估计；在对照组中，使用实验组的模型进行估计；使这两部分的估计尽量接近，从而使得实验组和对照组的分布尽量接近一致。混淆熵的使用是我们这个工作的主要贡献之一。

• 最终损失为以上两部分的加权和。注意到损失中主要使用的是干预前  的数据（经验损失部分仍会使用干预后的数据来拟合），即用干预前的数据进行辅助纠偏。

② 参数估计

• 参数估计使用的是干预后（t≥τ）的数据进行因果效应的估计。主要使用干预前的数据纠偏学习得到一个树结构，在叶子节点中使用干预后的数据进行因果效应的估计，由于使用干预前的数据进行了显式地纠偏，因此在使用干预后的数据计算得到的估计会更加准确。
• （PPT 的右侧）由右图所示，黄色的线代表实验组，蓝色的组代表对照组。业务中的一些策略可能会导致实验组和对照组的分配不是随机的，两者的分布存在明显的差异。经过 GBCT 纠偏后，叶子节点上干预前的实验组和对照组的数据分布基本是对齐的，从某种意义上达到了类似模拟随机对照实验的效果，因此使用干预后的数据估计因果效应（黄线下的面积减去蓝线下的面积）会更加准确。

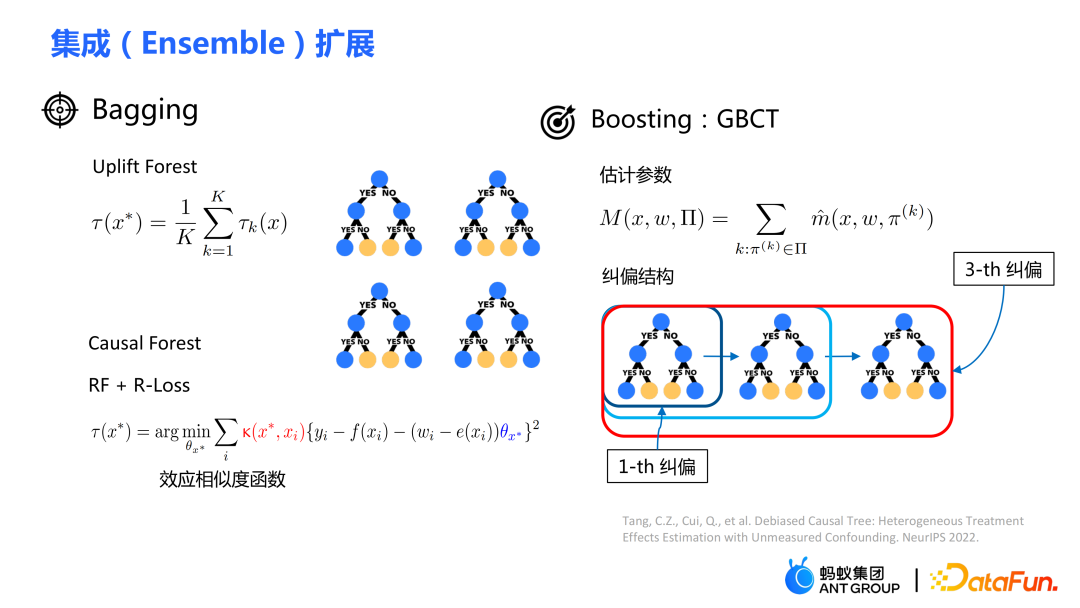
传统的树模型的集成包括 bagging、boost 等方法。uplift forest 或 causal forest 使用的集成方法为 bagging 法，uplift forest 的集成为直接求和，而causal forest 的集成需要求解一个损失函数。

由于在 GBCT 中设计了显式纠偏的模块，从而 GBCT 支持使用 boosting方法进行集成。基本思想与 boosting 类似：在第一棵树纠偏完之后，第二棵树进行纠偏，第三棵树进行纠偏……

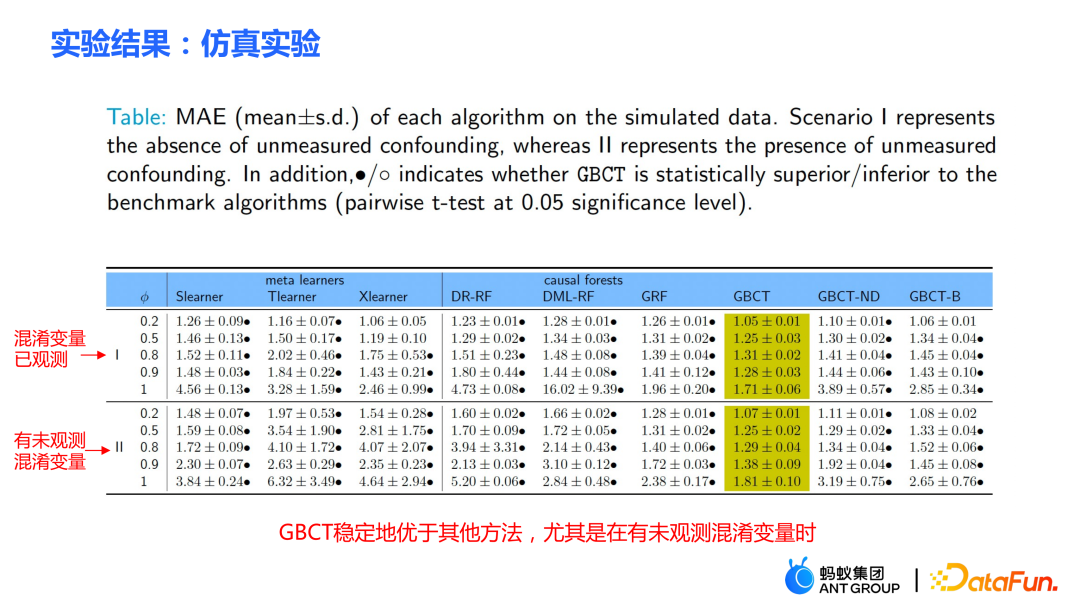
实验方面做了两部分实验：

① 仿真实验。在含有 ground truth 的仿真实验下，检验 GBCT 的方法是否能够达到预期的效果。仿真实验的数据生成分为两部分（表格中的第一列Φ表示选择偏倚，Φ值越大，对应的选择偏倚就越强；表格中的数值为 MAE，MAE 值越小表明方法越好）：

• 第一部分是混淆变量已观测。在混淆变量都已观测的情况下，检验 GBCT 的方法相对于传统方法是否更加鲁棒。由表中数据可得出结论，选择偏倚越大，传统方法（meta learner、causal forest 等）表现越差。
• 第二部分是存在未观测的混淆变量。此时很多传统方法的效果会显著地变差。对 GBCT 而言，在存在未观测混淆变量时表现比较稳定，同时稳定地比其他方法表现得好。
• 表格中最后两列（GBCT-ND, GBCT-B）是消融实验，即去掉一些模块的 GBCT 的弱化版本，进而说明我们提出的每个模块都是有用的。

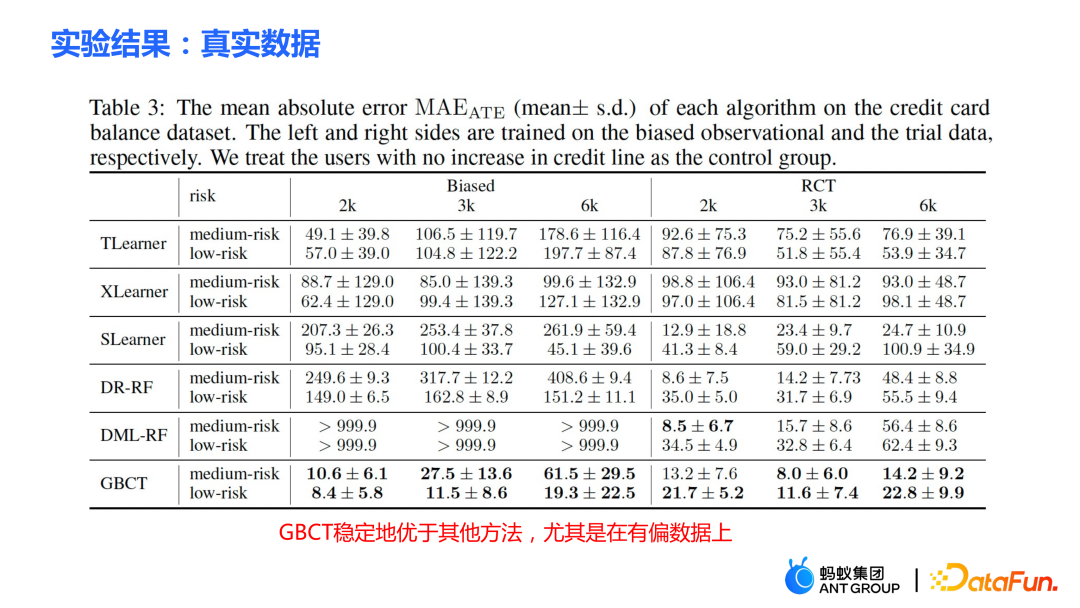
② 真实信用卡提额数据。进行随机对照的实验，同时根据随机对照实验构造了有偏数据。在不同的设置下，GBCT 方法比传统的方法稳定地好，尤其是在有偏的数据上，显著比传统的方法表现得好。

三、因果数据融合

第二个工作是因果数据融合，即在拥有多个数据源的情况下，如何更好地估计因果效应。

主要的符号：是多个数据源，Y 是outcome，A 是treatment，X 是关注的协变量，Z 是除 X 了外每个数据源（域）的其他协变量，S 是域的indicator用于表示属于哪个域，μ 是潜在结果的期望值。将outcome拆解成如下表达式：

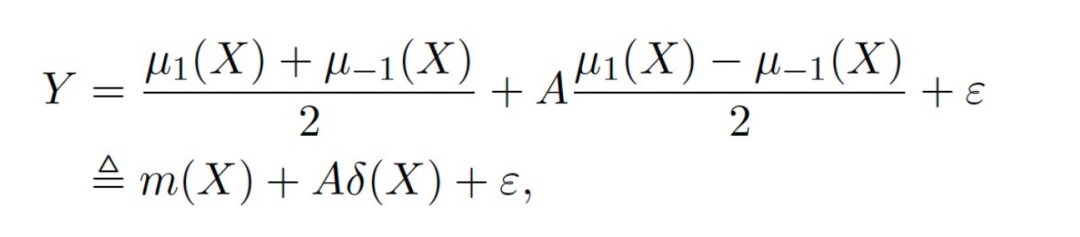
target function δ 用于估计每个域上的因果效应，另外 nuisance functions 包括主效应、倾向性评分、域倾向性评分、效应的方差等。

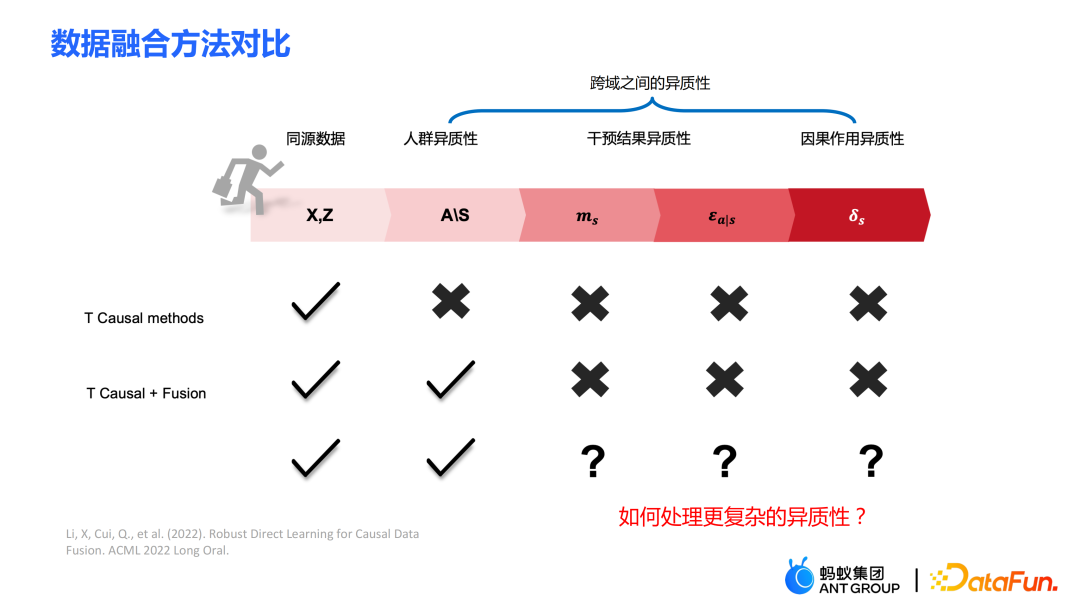
一些传统的方法，比如 meta learner 等都是假设数据是同源的，即分布是一致的。一些传统的数据融合方法可以处理在跨域之间人群的异质性，但是无法显式地捕捉到干预结果跨域的异质性以及因果作用跨域的异质性。我们的工作主要是处理更复杂的跨域间的异质性，包括干预结果跨域之间的异质性以及因果作用跨域之间的异质性。

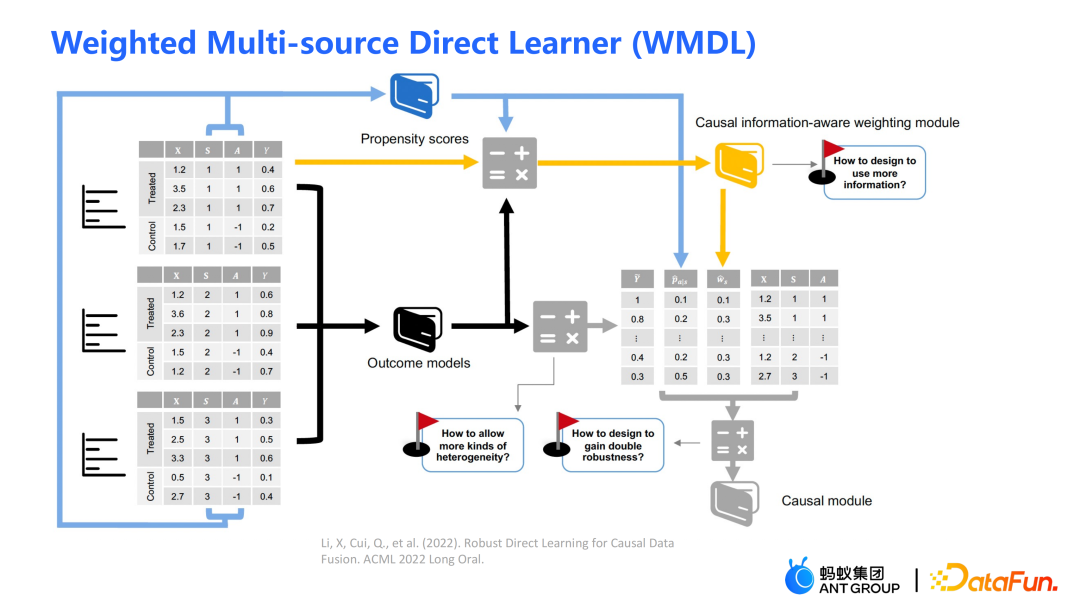
WMDL 算法的框架图如上图所示。主要的模块为：

• propensity scores
• outcome models
• causal information-aware weighting module

三个模块综合起来就得到了最终的估计。WMDL 算法的三个亮点为：

• 如何刻画不同程度的跨域之间的异质性
• 如何设计 weighting 的模块以用上更多的信息
• 如何得到一个 doubly robust 的估计

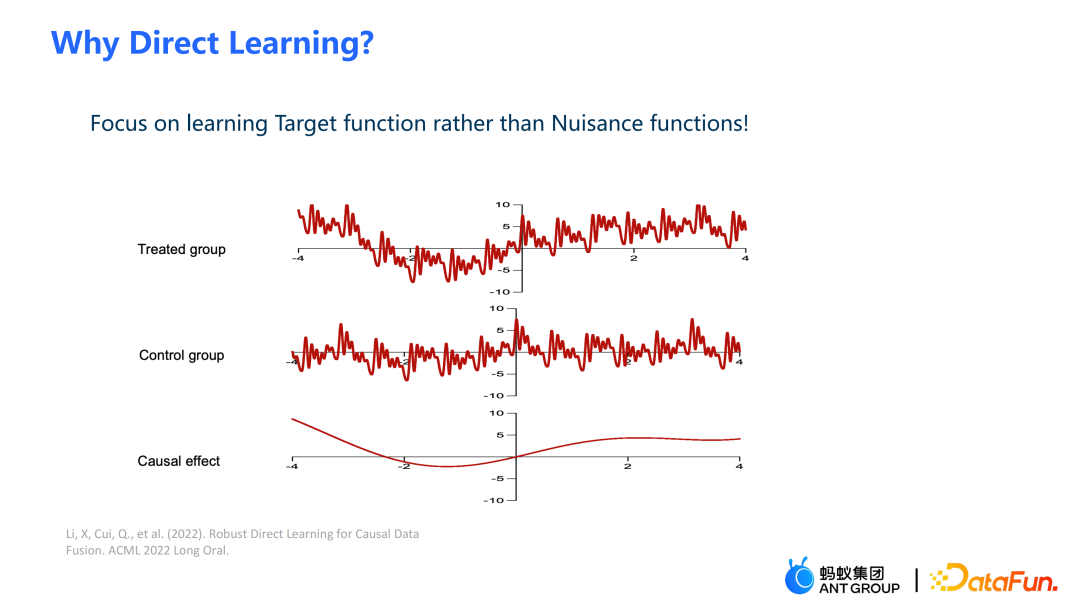
在本次工作中不是通过估计实验组的 outcome 和对照组的 outcome，然后作差得到因果效应的估计，而是直接估计因果效应，即 Direct Learning。Direct Learning 的好处是可以避免实验组和对照组中较高频的噪声信号。

左边部分假设了多个域之间因果效应是一样的，但其 outcome 可能存在异质性；右边部分假设每个域之间的因果效应不一样，即在不同的域之间，即使它的协变量一样，其因果效应也不同。

公式是根据拆解式推导得到的，outcome Y 减去 main effect 除以treatment，估计的是 I(X)，得到的最优解即为 δ(X)。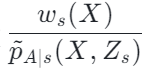中的分子是后面将要提到的 causal information-aware weighting module，是我们本次工作的一个主要贡献点；分母则类似于 doubly robust 方法中的倾向性得分，只不过本次工作中同时考虑了域的信息。如果不同域之间的因果效应不一样，会同时考虑域的 indicator 信息。

本次工作三方面的优势：

① 通过不同的设计，不仅能处理干预结果的异质性，同时可以处理因果作用之间的异质性；

② 具有 doubly robustness 性质。在论文中给出了证明，只要域的倾向性评分模型或主效应模型两者之一的估计是无偏的，最终得到的估计就是无偏的（实际情况略复杂一点，细节见论文）；

③ 本次工作主要设计了半参模型框架。其中模型的每一个模块都可以用任何机器学习的模型，甚至可以将整个模型设计进神经网络中，实现端到端的学习。

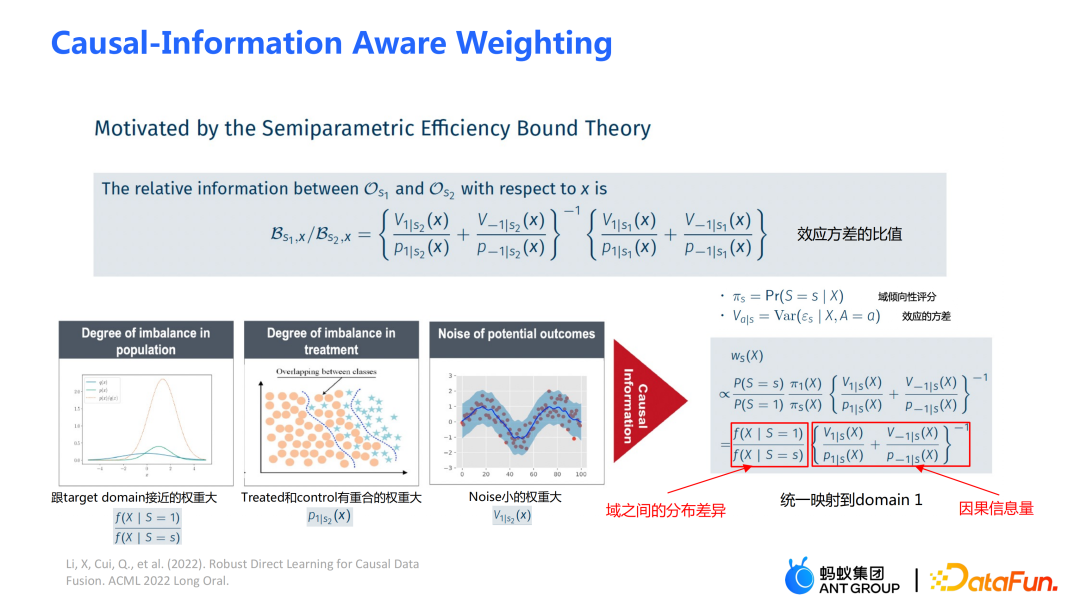
Weighting 的模块是从统计学中的 efficiency bound theory 推导得到的。主要包含两方面信息：

① 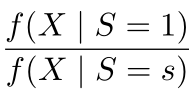是域之间分布差异平衡转换的模块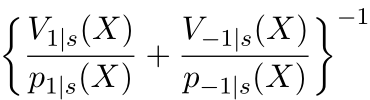；是因果相关的信息量模块。可通过左边三幅图来辅助理解：如果源域（source domain）和目标域（target domain）之间分布的差异较大，则优先给与目标域（target domain）较接近的样本以较大的权重；

② 通过分母上的倾向性评分函数的设计，给实验组和对照组中存在重叠（overlap）的这部分样本以较大的权重；

③ 通过 V 刻画数据中的噪声。由于噪声在分母上，噪声小的样本将得到较大的权重。

通过巧妙地将上述三部分结合在一起，可以将不同域之间的分布差异以及不同因果信息的表现映射到统一的域中。

不管在同质的因果效应还是异质的因果效应下，WMDL（Weighted Multi-domain Direct Learning）方法都有较好的效果。右图则是对 weighting 模块进行了消融实验，实验表明了 weighting 模块的有效性。综上所述，WMDL 方法稳定地比其他方法效果好，估计的方差比较小。

四、在蚂蚁的业务应用

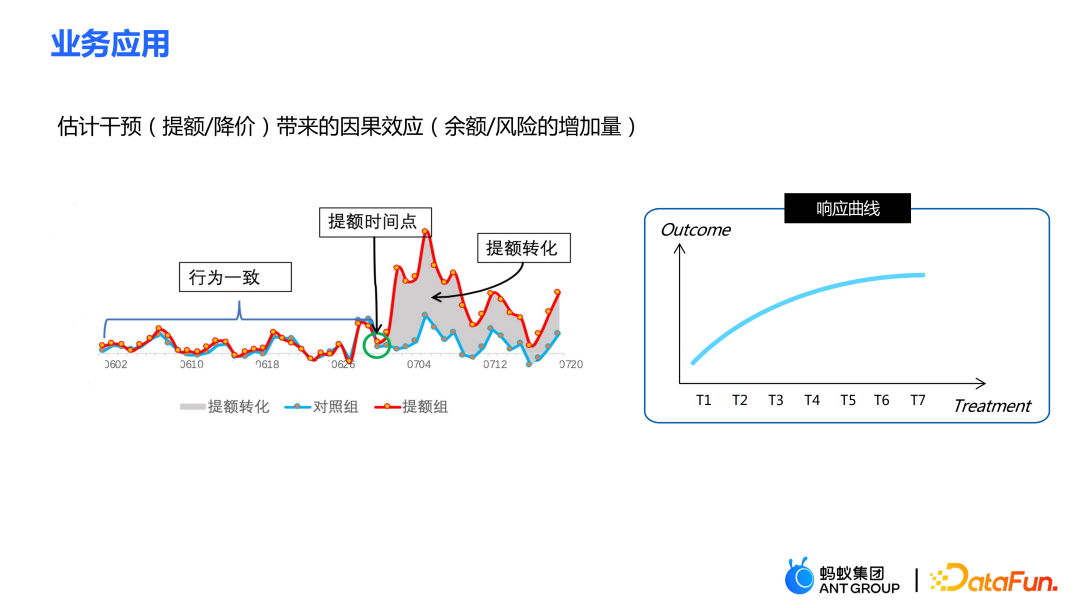
在金融信贷风控场景中，干预的手段如提额、降价等，希望得到预期的效果如余额或风险的变化量。在一些实际的场景中，GBCT 的纠偏工作会利用提额前一段时间内的历史表现（实验组和对照组在不提额下的状态可获得），通过历史的信息进行显式纠偏，使得干预后的估计会更加准确。GBCT 分裂到一个子节点，使得干预前行为对齐，则干预后的因果效应就比较容易估计了。（纠偏后得到的）图中红色为提额组，蓝色为不提额组，中间的灰色区域即为估计的因果效应。GBCT 帮助我们更好地做出智能决策，控制信贷产品的余额及风险。

五、问答环节

Q1：请问 GBCT 纠偏和双重差分方法（DID）有何异同？

A1：GBCT 纠偏主要思想是利用历史对照信息显式地降低选择偏倚，GBCT 的方法和 DID 双重差分的方法有相似也有不同之处：

• 相似的地方是二者都利用了历史信息；
• 不同的地方在于两者对于历史信息的处理方式。DID 假设历史数据中的实验组和对照组之间存在固定常值的间隔（gap），在预测时减去间隔（gap）。由于选择偏倚，实验组和对照组的分配不是随机的，GBCT 通过纠偏的方式，将历史的实验组和对照组进行对齐。

Q2：GBCT 在未观测混淆变量上会表现得更好，有什么比较直观的解释？

A2：如果所有的混淆变量已观测的话，满足可忽略性（Ignorability）假设，某种程度上，虽然没有显式地降低选择偏倚，实验组和对照组也有可能通过传统的方法实现对齐，实验表明 GBCT 的表现要略胜一筹，通过显式纠偏使得结果更稳定一些。

假设存在一些未观测到的混淆变量，此类场景在实际中是非常常见的，历史的对照数据中也存在未观测的混淆变量，比如在提额前，家庭情况、收入的变化等可能观测不到，但是用户的金融行为已经通过历史数据体现出来了。我们希望通过历史的表现信息，以混淆熵等方式显式降低选择偏倚，使得在树分裂时，将混淆变量之间的异质性刻画到分裂的子节点中。在子节点中，使得未观测的混淆变量有更大的概率是比较相近的，因此估计的因果效应相对更准确。

Q3：有将 GBCT 和 Double Machine Learning（DML）做过比较吗？

A3：做过比较。Double Machine Learning 是一个半参的方法。我们这篇工作更关注于 tree-based 方法，所以选用的 base learner 都是一些 tree 或 forest 等相关的方法。表格中的 DML-RF 是 Double Machine Learning 版的 Random Forest。 

相比于 DML，GBCT 主要是在考虑如何利用历史的对照数据。在对比方法中，会把历史的 outcome 直接作为协变量处理，但这种处理方法显然没有把信息用得很好。

Q4：业务中可能会遇到的比较相似的问题是，离线可能会有选择偏倚。但是线上的偏倚可能会和离线的偏倚存在一些偏差。此时在离线做效果评估时，可能没有办法非常准确地对离线效果进行估计。

A4：这个问题在金融场景是一个非常本质的问题。在搜推广中可以通过在线学习或者 A/B test 部分克服离线与在线之间的差异。在金融场景，受政策影响不能轻易地在线上做实验；另外表现的观测周期通常较长，如信贷产品观察到用户的反馈需要至少 1 个月的观测时间。因此实际上很难完美地解决这个问题。

我们一般采取如下方式：在离线评估时使用不同时期（OOT）的测试数据去做验证，观察其表现的鲁棒性。如果测试表现比较稳定的，那么相对来说更有理由相信其在线上的表现也是不错的。