图机器学习无处不在，用 Transformer 可缓解 GNN 限制

在我们今天的生活中，图的示例包括社交网络、例如Twitter、Mastodon、以及任何链接论文和作者的引文网络，分子，知识图、例如 UML 图、百科全书以及有超链接的网站，表示为句法树的句子以及任何的 3D 网格等，可以说图已经无处不在。

近日，Hugging Face 研究科学家 Clémentine Fourrier 在文章《Introduction to Graph Machine Learning》就介绍了今天这种无处不在的图机器学习。什么是图形？为什么要使用图？如何最好地表示图？人们如何在图上学习？Clémentine Fourrier 指出，图是对由关系链接项目的描述，其中，从前神经方法到图神经网络仍然是目前人们常用的图上学习方法。

此外，有研究人员近期也开始考虑将 Transformers 应用于图中，Transformer 具有良好的可扩展性，可缓解 GNN 存在的部分限制，前景十分可观。

1 图是对关系链接项目的描述

从本质上来看，图是对由关系链接项目的描述。图（或网络）的项目称为节点（或顶点），由边（或链接）来进行连接。例如在社交网络中，节点是用户，边是用户彼此间的连接；在分子中，节点是原子，边缘是它们的分子键。

• 一个有类型节点或类型边的图被称为异质图，举个例子，在引文网络的项目可以是论文或作者，有类型节点，而 XML 图中的关系有类型边；它不能仅仅通过其拓扑结构来表示，还需要额外的信息
• 图也可以是有向的（例如追随者网络，A 跟随 B 并不意味着 B 跟随 A）或无向的（例如分子、原子之间的关系是双向的）。边可以连接不同的节点或一个节点与自身（自边），但并非所有节点都需要连接

可以看到，使用数据必须首先考虑其最佳表示，包括同质/异质、有向/无向等。

在图层面，主要任务包括以下：

• 图形生成，用于药物发现以生成新的合理分子
• 图演化，即给定一个图来预测它将如何随时间演化，在物理学中可用于预测系统的演化
• 图级预测，来自图的分类或回归任务，例如预测分子的毒性

节点层通常是对节点属性的预测，例如 Alphafold 使用节点属性预测来预测给定分子整体图的原子 3D 坐标，从而预测分子如何在 3D 空间中折叠，这是一个困难的生物化学问题。

边缘的预测包括边缘属性预测和缺失边缘预测。边缘属性预测有助于对药物副作用的预测，给定一对药物的不良副作用；缺失边预测在推荐系统中则是用于预测图中的两个节点是否相关。

在子图级别中，可进行社区检测或子图属性预测。社交网络可通过社区检测来确定人们的联系方式。子图属性预测多应用在行程系统中，例如谷歌地图，可用于预测预计到达时间。

当要进行预测特定图的演变时，转换设置工作中的所有内容，包括训练、验证和测试等，都可在同一个图上完成。但从单个图创建训练、评估或是测试的数据集并非易事，很多工作会使用不同的图（单独的训练/评估/测试拆分）完成，这被称为归纳设置。

表示图处理和操作的常见方法有两种，一种是作为其所有边的集合（可能由其所有节点的集合补充），或是作为其所有节点之间的邻接矩阵。其中，邻接矩阵是一个方阵（节点大小×节点大小），指示哪些节点直接连接到其他节点。要注意的是，由于大多数图并不是密集连接的，因此具有稀疏的邻接矩阵会使计算更加困难。

图与 ML 中使用的典型对象非常不同，由于其拓扑结构比“序列”（如文本和音频）或“有序网格”（如图像和视频）更复杂：即便可以将其表示为列表或矩阵，但这种表示不可以被视为是有序对象。也即是说，如果打乱一个句子中的单词，就可以创造一个新句子，如果将一个图像打乱并重新排列它的列，就能创建了一个新图像。

图注：Hugging Face 标志和被打乱的 Hugging Face 标志，是完全不同的新形象

但图的情况并非如此：如果我们洗掉图的边缘列表或邻接矩阵的列，它仍然是同一个图。

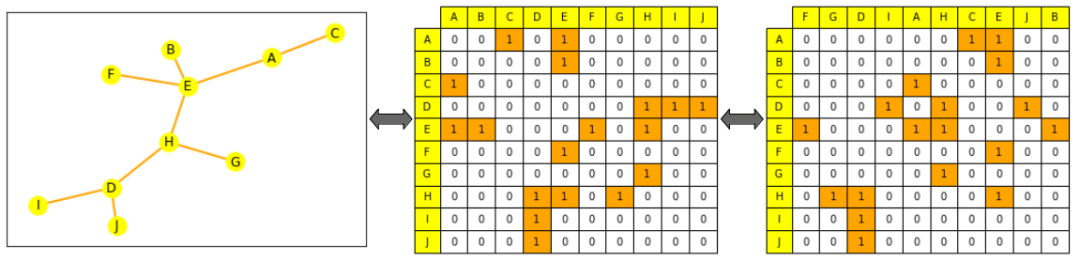
图注：左边是一个小图，黄色表示节点，橙色表示边；中心图片上的邻接矩阵，列和行按节点字母顺序排列：节点 A 的行（第一行）可以看到其连接到 E 和 C；右边图片打乱邻接矩阵（列不再按字母顺序排序），其仍为图形的有效表示，即 A 仍连接到 E 和 C

2 通过 ML 的图形表示

使用机器学习处理图的常规过程，是首先为项目生成有意义的表示，其中，节点、边或完整图取决于具体任务需求，为目标任务训练预测器。与其他模式一样，可以通过限制对象的数学表示，以便在数学上与相似对象接近。但在此之中，相似性在图 ML 中很难严格定义：例如，当两个节点具有相同的标签或相同的邻居时，它们是否更相似？

如下面所示，本篇文章重点关注的是生成节点表示，一旦有了节点级的表示，就有可能获得边或图级的信息。对边级信息，可以将节点对的连接起来，或者做点乘；在图级信息中，可以对所有节点级表示的串联张量进行全局池化，包括平均、求和等。但是，它仍然会使整个图的信息变得平滑和丢失——递归的分层集合可能更有意义，或者增加一个虚拟节点，与图中的所有其他节点相连，并将其表示作为整个图的表示。

前神经方法

简单地使用工程特性

在神经网络之前，图形及其感兴趣的项目可以通过特定任务的方式表示为特征的组合。在今天，这些特征仍用于数据增强和半监督学习，尽管存在更复杂的特征生成方法，但根据任务找到如何最好地将这些特征提供给到网络至关重要。

节点级特征可以提供关于重要性的信息以及基于结构的信息，并对其进行组合。

节点中心性可用于衡量图中节点的重要性，通过对每个节点邻居中心性求和直到收敛来递归计算，或是通过节点间的最短距离度量来递归计算，节点度是其拥有的直接邻居的数量；聚类系数衡量节点邻居的连接程度；Graphlets 度向量计算则可计算有多少不同的 graphlets 以给定节点为根，其中，graphlets 可使用给定数量的连接节点来创建的所有迷你图。

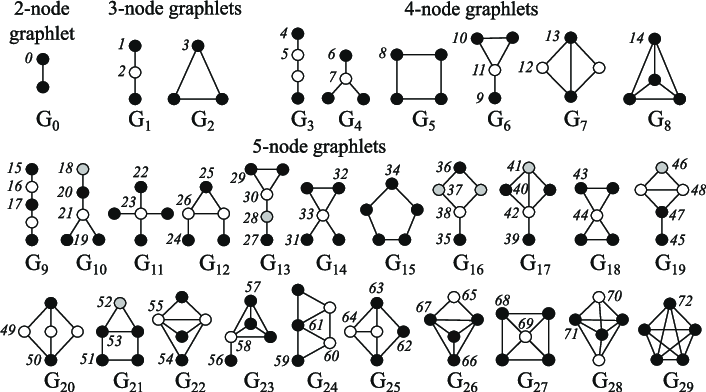
图注：2 到 5 节点小图

边级特征用关于节点连通性的更详细信息补充表示，其中就包括了两个节点之间的最短距离、它们的共同相邻点以及 Katz 指数（指两个节点之间可能走过的一定长度的路径的数量——其可以直接从邻接矩阵中计算出来）。

图级特征包含关于图相似性和特殊性的高级信息，其中，小图计数，尽管计算成本很高，但提供了关于子图形状的信息。核心方法通过不同的 “节点袋 “方法（类似于词袋）来衡量图之间的相似性。

基于行走的方法

基于行走的方法使用随机行走中从节点 i 访问节点 j 的概率来定义相似性度量，这些方法结合了局部和全局信息。例如，此前 Node2Vec 模拟图形节点之间的随机游走，使用 skip-gram 处理这些游走，就像我们处理句子中的单词一样，以计算嵌入。

这些方法还可用于加速 PageRank 方法的计算，该方法给每个节点分配一个重要性分数，基于它与其他节点的连接，例如通过随机行走来评估其访问频率。但上述方法也存在一定的局限性，它们不能获得新节点的嵌入，不能很好地捕捉节点之间的结构相似性，不能使用添加的特征。

3 图神经网络如何处理图？

神经网络可以泛化到看不见的数据。考虑到此前提到的表示约束，一个好的神经网络应该如何处理图？

下面展示了两种方法：

• 是置换不变的：

• 方程：f（P（G））=f（G）f（P（G））=f（G） ，其中 f 是网络，P 是置换函数，G 是图
• 解释：经过网络后，图的表示及其排列应该相同

• 是置换等变的

• 方程：P（f（G））=f（P（G））P（f（G））=f（P（G）），其中 f 是网络，P 是置换函数，G 是图

• 解释：在将节点传递到网络之前置换节点应该等同于置换它们的表示

典型的神经网络不是排列不变的，例如 RNN 或 CNN，因此一种新的架构——图神经网络被引入（最初是作为一种基于状态的机器）。

一个 GNN 是由连续的层组成的。GNN 层将节点表示为其邻居的表示和来自上一层（消息传递）的自身组合 ，通常还会加上激活以添加一些非线性。而与其他模型相比，CNN 可看作是具有固定邻居大小（通过滑动窗口）和排序（非排列等变）的 GNN；而没有位置嵌入的 Transformer 可以看作是全连接输入图上的 GNN。

聚合和消息传递

聚合来自节点邻居的信息有很多方法，例如求和、平均，此前已有的类似聚类方法包括：

• Graph Convolutional Networks，对节点邻居的归一化表示进行平均；
• Graph Attention Networks，学习根据它们的重要性来权衡不同邻居（如Transformer）；
• GraphSAGE，在使用最大集合在几个步骤中聚合信息之前，在不同的跃点对邻居进行采样；
• Graph Isomorphism Networks，通过将 MLP 应用于节点邻居表示的总和来聚合表示。

选择一个聚合：一些聚合技术（特别是平均/最大集合）在创建精细表示以区分类似节点的不同节点邻居表示时，会遇到失败的情况；例如，通过均值集合，一个有4个节点邻居表示为1、1、-1、-1，平均为0，与一个只有3个节点表示为-1、0、1的邻居是没有区别的。

GNN 形状和过度平滑问题

在每个新层，节点表示包括越来越多的节点。一个节点通过第一层，是其直接邻居的聚合。通过第二层，它仍然是其直接邻居的聚合，但此刻其表示还包括了它们自己的邻居（来自第一层）。在 n 层之后，所有节点的表示成为其距离为 n 的所有邻居的集合，因此，如果其直径小于n，则为全图的聚合。

如果网络层数太多，则存在每个节点成为完整图的聚合的风险（并且节点表示对所有节点收敛到相同的表示），这被称为过度平滑问题，可通过以下方式来解决：

• 将 GNN 缩放到足够小的层数，从而不会将每个节点近似为整个网络（通过首先分析图的直径和形状）
• 增加层的复杂性
• 添加非消息传递层来处理消息（例如简单的 MLP）
• 添加跳过连接

过度平滑问题是图 ML 中的一个重要研究领域，由于它会阻止 GNN 扩大规模，就像 Transformers 在其他模型中被证明的那样。

图 Transformers

没有位置编码层的 Transformer 是置换不变的，并且 Transformer 还具有良好的可扩展性，因此研究人员在近期开始考虑将 Transformers 应用于图中。大多数方法的重点是通过寻找最佳特征和最佳方式来表示图形，并改变注意力以适应这种新数据。

下面展示了一些方法，这些方法在斯坦福大学的 Open Graph Benchmark 上取得最先进或接近的结果：

• Graph Transformer for Graph-to-Sequence Learning，引入一个图 Transformer，它将节点表示为它们的嵌入和位置嵌入的串联，节点关系表示二者间的最短路径，并将两者组合成一个关系——增强自我关注。
• Rethinking Graph Transformers with Spectral Attention，引入了 Spectral Attention Networks （SAN），这些将节点特征与学习的位置编码（从拉普拉斯特征向量/值计算）结合起来，用作注意力中的键和查询，注意力值是边缘特征。
• GRPE: Relative Positional Encoding for Graph Transformer，介绍了图相对位置编码Transformer，其通过将图级位置编码与节点信息、边级位置编码与节点信息相结合，并将两者结合在注意力中来表示图。
• Global Self-Attention as a Replacement for Graph Convolution ，引入了 Edge Augmented Transformer，该体系结构分别嵌入节点和边缘，并将它们聚合在经过修改的注意力中。
• Do Transformers Really Perform Badly for Graph Representation，介绍了微软的 Graphormer，它在 OGB 上问世时获得了第一名。该架构使用节点特征作为注意力中的查询/键/值，并在注意力机制中将它们的表示与中心性、空间和边缘编码相结合。

近期有研究“Pure Transformers are Powerful Graph Learners”在方法中引入了 TokenGT，将输入图表示为一系列节点和边嵌入，也即是使用正交节点标识符和可训练类型标识符进行增强，没有位置嵌入，并将此序列作为输入提供给 Transformers，此方法非常简单，同时也非常有效。

论文地址：https://arxiv.org/pdf/2207.02505.pdf

此外，在研究“Recipe for a General, Powerful, Scalable Graph Transformer”中，跟其他方法不同的是，它引入的不是模型而是框架，称为 GraphGPS，可允许将消息传递网络与线性（远程）Transformer 结合起来，轻松创建混合网络。该框架还包含几个用于计算位置和结构编码（节点、图形、边缘级别）、特征增强、随机游走等的工具。

论文地址：https://arxiv.org/abs/2205.12454

将 Transformer 用于图在很大程度上仍处于起步阶段，但就目前来看，其前景也十分可观，它可以缓解 GNN 的一些限制，例如缩放到更大或更密集的图，或是在不过度平滑的情况下增加模型大小。