首个二值量化评测基准来了,北航/NTU/ETH联合提出,论文登ICML 2023
本文经AI新媒体量子位(公众号ID:QbitAI)授权转载,转载请联系出处。
二值量化可以有效节约AI模型消耗的资源。
具体而言,它可以把32位浮点数值压缩到1位,大大降低了存储和运算成本。
然而,此前对二值量化模型质量的评测一直停留在理论层面,难以对算法在准确性和效率方面的表现进行全面评估。
为此,来自北京航空航天大学、南洋理工大学、苏黎世联邦理工大学的研究者,全新推出了首个二值量化评测基准BiBench。

相关论文已被ICML 2023接收。
近日,机器学习顶会 ICML 2023接收论文结果已经正式公布。在 6538篇有效投稿中,最终有1827篇论文被接收,录取率约为 27.9%。
论文地址:https://arxiv.org/abs/2301.11233
项目地址:https://github.com/htqin/BiBench
背景及概述
随着深度学习的兴起,较大模型的高资源需求与部署资源限制之间的矛盾持续加剧,模型压缩技术被广泛研究以解决这一问题。
神经网络二值化作为将模型参数位宽减少到1位的压缩方法,被视为最极致的量化技术,能够极大地降低模型存储开销,并通过高效的位运算加速模型推理。
然而,现有的神经网络二值化算法仍然远非实用,局限主要存在于两方面:
1) 模型精度评估范围有限:目前的大部分工作主要都在CIFAR-10以及ImageNet这类2D图像分类任务上展开的,同时数据噪声在二值化算法的评估中也时常被忽略;
2) 效率分析仍停留在理论层面:由于缺乏二值神经网络部署库,大部分工作对于二值化算法的压缩以及加速效果主要停留在理论分析层面。
精度和效率相关对比标准的缺失使得新二值化算法的贡献逐渐模糊,架构通用的二值算子改进很难在对比中脱颖而出,而这本应是模型量化类技术的主要优势。

△ 图 1: BiBench评估轨道与结果
为了解决以上的这些问题,本文提出了BiBench (Binarization Benchmark),这是一个神经网络二值化算法评测基准,旨在全面评估二值化算法在准确性和效率方面的表现。
BiBench评估了8个基于算子级别并具有广泛影响力的代表性二值化算法,并在9个深度学习数据集、13个神经架构、2个部署库、14个硬件芯片以及各种超参数设置下对算法进行了基准测试。
BiBench消耗了约4个GPU年的计算时间来完成实际测试,全面地评估了神经网络二值化算法,并针对基准的测试结果进行了深入的分析,为设计实用的二值化算法提供了有效建议。
评估轨道及指标
如图1所示,BiBench的评估主要包含了面向精度的评测以及面向效率的评测这两个方面,共计六个评测轨道,每个轨道都有相应的评测指标,有效地解决了在生产和部署二值化网络中面临的实际挑战。
面向精度的二值化算法评估
在面向精度的二值化算法评估中,主要包括了“学习任务”,“网络架构”和“扰动鲁棒性”这三个评测轨道。

学习任务
在“学习任务”这一轨道上,本文详尽地评测了二值化算法在四个模态共计九个深度学习数据集上的性能表现。
在2D视觉模态上,本文评估了在CIFAR-10和ImageNet数据集上的图像分类任务,在PASCAL VOC以及COCO数据集上的目标检测任务。
在3D视觉模态上评估了在ModelNet40数据集上的3D点云分类任务以及在ShapeNet数据集上的3D点云分割任务。
在文本模态评估了在GLUE 基准上的自然语言理解任务。在语音模态评估了在Speech Commands KWS dataset上的语音识别任务。
为了定量地评估不同二值化算法在这个轨道上的性能表现,本文将对应的全精度神经网络的准确率作为了基线,并计算了所有任务上所有架构的平均相对准确率。
所有任务的相对准确率的二次均值作为该轨道的整体指标,计算公式如下:

其中和分别代表了二值化模型和全精度模型在第i个任务上的准确率。
网络架构
在“网络架构”这一轨道上,本文评估了多种神经网络架构,包括主流的基于卷积神经网络(CNN)的架构,基于Transformer的架构以及基于多层感知机(MLP)的架构。
具体来说,本文将标准的ResNet-18/20/34以及VGG作为了基于卷积神经网络的评估架构,并将Faster-RCNN以及SSD300框架作为了目标检测任务中的检测器。
对于基于Transformer的架构使用了bi-attention机制二值化了BERT-Tiny4/Tiny6/Base模型以便于收敛。
同时也评估了多种基于多层感知机(MLP)的架构,包括了PointNetvanilla, 带有EMA聚合器的PointNet, FSMN以及Deep-FSMN.
和“学习任务”轨道类似,在“网络架构”轨道上,本文也使用了相似的整体指标,其计算公式如下:

扰动鲁棒性
在部署时,二值化的扰动鲁棒性对于应对某些场景(如感知设备损坏)至关重要,这在现实世界中边缘设备的应用中是一个常见问题。
因此,本文同时也评估了二值化算法在CIFAR10-C 基准上的表现,用于评估二值化模型在2D视觉数据损坏情况下的鲁棒性,其整体指标计算公式如下:
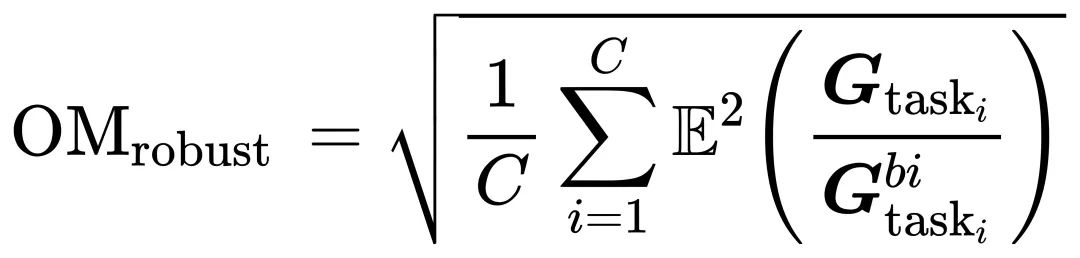
在这里

代表了扰动泛化差距,其中

和

分别表示在第i个扰动任务和相应的正常任务下,所有架构的准确性结果。

面向效率的二值化算法评估
在面向效率的二值化算法评估中,主要包括了“训练开销”,“理论复杂度”和“硬件推理”三个评测轨道。
其中“训练开销”轨道主要评估二值化算法的生产效率,而其余两个轨道评估了二值化算法的部署效率。

训练开销
在“训练开销”轨道上,本文主要考虑了二值化算法所占用的训练资源和对超参数的敏感性,这些因素影响单次训练的消耗和整体调优过程。
为了评估调整二值化算法以达到最佳性能的难易程度,本文使用不同的超参数设置训练二值化网络,包括不同的学习率、学习率调度器、优化器甚至随机种子,将二值化网络和全精度网络的训练轮次对齐,并比较了它们的消耗和时间。
定量的整体指标的计算公式如下:
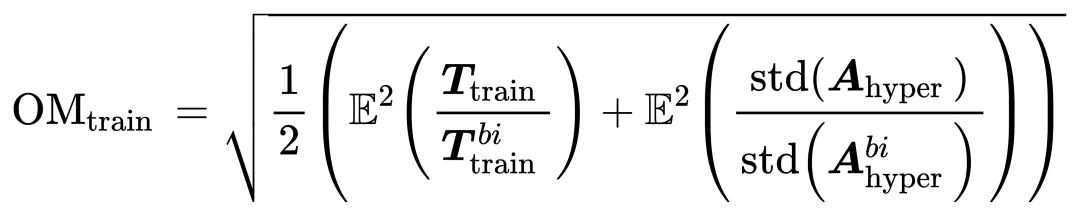
其中

表示单次训练实例所花费的时间,

是使用不同超参数配置获得的准确率。
理论复杂度
在“理论复杂度”这一轨道上,本文主要计算模型二值化前后模型的压缩比合加速比,理论复杂度的总体指标的计算公式如下:
其中

和

分别代表了二值化算法的压缩比和加速比,二值化参数由于只占据1个bit,相较于32位浮点数只占据1/32的存储空间;
而二值化模型在推理过程中,仅包含1位权重乘以1位激活值的开销,在具有64位指令大小的CPU上需要大约1/64的FLOPs(floating point operations per second),因此二值化算法的压缩比和加速比的计算方式如下:

其中

和

分别是原始模型和二值化模型中保留的全精度参数的数量,

和

代表了模型的计算力。
硬件推理
由于二值化算法在硬件部署库上尚未得到广泛支持,目前仅有两个常用推理库 – Larq Compute Engine 和京东的 daBNN 提供了完整的流程以将二值化模型实际部署到 ARM 硬件上。
因此,本文主要依据这两个推理库,评估了二值化模型在边缘场景下主流硬件上的 ARM CPU 推理性能,如华为麒麟,高通骁龙,苹果 M1,联发科天玑和树莓派。
对于给定的二值化算法,使用不同推理库和硬件下的存储和推理时间节省作为评估指标,总体评估指标计算方式如下:

其中

是模型的推理时间,

是模型在不同设备上的存储开销。
评估及分析
BiBench从二值算法的准确性和效率两方面,全面地评估了所选二值算法的性能表现。
二值算法的准确性分析
本文分别针对不同任务、针对不同模型架构、针对扰动鲁棒性三个轨道,评估了各二值算法的准确率。上表汇报了基于相关性度量的模型准确率表现。
从学习任务的角度
模型准确率仍然是目前二值算法研究中最具挑战性的难题。
BiBench将训练流程和模型架构完全统一,以此来观察不同二值算法的表现。
发现在大多数任务中,二值算法的准确率表现仍然是有限的。在大规模视觉数据集ImageNet和COCO上,二值模型的准确率往往是对应的全精度模型的不到80%。
而且,准确率的边际效应在二值算法中已经出现,比如,在ImageNet数据集上,最先进的ReCU算法比最朴素的BNN算法准确率仅仅高了3%。
二值算法在不同数据模态下的表现差异很大。
二值算法在文本理解任务GLUE数据集上的精度降低非常严重,然而在点云分类的ModelNet40数据集上却有与全精度模型相媲美的准确率表现。
这表明,二值化的研究中得到的经验和启迪,很难在不同模态的任务下直接移用。
总体来说,ReCU和ReActNet在各种不同的任务下都取得了较高的准确率表现,ReCU在4个独立的任务中获得了准确率的第一,而ReActNet获得了总体准确率的第一。
两个算法都在前向过程中采用了重参数化,在反向过程中采用了梯度近似的方法。
从网络架构的角度
二值算法在CNN和MLP架构上的表现相比在Transformer架构上具有明显的优势。
由于二值算法在CNN架构相关的模型上已有广泛的研究,一些先进的二值算法通常能达到相比于全精度模型78%~86%的准确性。
而MLP架构上的二值算法甚至能达到接近全精度模型的准确率表现(例如Bi-Real Net达到87.83%)。
与之形成鲜明对比的是,在二值化Transformer架构时却受到了严重的精度降低,甚至没有一个算法的整体相对准确率能够超过70%。
这个好结果表明,相比于CNN和MLP架构的模型,Transformer架构由于其特殊的注意力机制,对二值化方法带来了更严峻的挑战,现有的对该机制的二值化方法还没有彻底解决这个问题。
在“网络架构”轨道上获得冠军的是FDA算法,它在CNN和Transformer架构上都获得了最好的准确率成绩。
关于任务和模型架构的这两个轨道的结果表明,像FDA和ReActNet的二值算法具有一定的稳定性,这两个算法都使用了逐通道的缩放参数和自定义的梯度近似方案。
从扰动鲁棒性的角度
二值模型能够达到与全精度模型同等的鲁棒性。
令人惊讶的是,虽然二值模型表现出了相对有限的表征能力和比较明显的准确率下降,但是在干扰数据集上,他们却展现出了与全精度模型同等的鲁棒性。
在CiFAR10-C数据集上,二值算法在常规2D损毁图像上的表现接近于全精度模型,而且ReCU和XNOR-Net算法的表现甚至超过了全精度模型。
这个事实表明,二值模型几乎不需要额外的训练或监督,就能达到与全精度模型同等的鲁棒性。
同时,各种二值化算法具有相似的鲁棒性表现,因此可以将鲁棒性视为二值模型的一般属性,而不仅仅属于特定算法。
二值算法的效率分析
BiBench分别从“训练开销”、“ 理论复杂度”、“ 硬件推理”三个轨道,全面评估了不同算法的效率。
训练开销

△ 图 2: 不同算法的参数敏感性
本文以CIFAR10数据集上的ResNet18为代表,全面地评估了二值算法的训练开销。上图和上表展示了不同二值算法的参数敏感性以及训练时间。
二值化并不意味着敏感:现有的技术能够稳定地训练二值算法。
一个现有的共同的直觉是,由于二值算法高度的离散性带来的表征能力有限和梯度近似的误差,二值模型的训练可能比全精度模型的训练更加敏感。
但是,本文发现现有二值算法对于超参数的敏感性是两极分化的,部分二值算法比全精度模型对于超参数具有更好的稳定性,而另一些二值算法则对超参数具有较大的性能波动。
对此,不同的二值技术有不同的原因。
本文总结出训练过程稳定的二值算法通常具有以下这些共性:
(1) 基于学习或统计量的逐通道浮点缩放因子;
(2) 降低梯度误差的梯度近似软函数。
这些对于超参数稳定的二值算法可能并不能获得比其他算法更好的模型准确率,但是它们能够在模型生产阶段简化训练/微调的过程,在单次训练后获得更可靠的准确性。
二值算法训练过程对于超参数的偏好是很明显的。
从图2中所示的结果来看,Adam优化器、与全精度相同的初始学习率 (1x) 和余弦退火的学习率策略训练得到的二值模型的表现能够稳定地优于其他超参数训练得到的模型。
受此启发,本文使用了这组表现最好的超参数作为标准训练流程的一部分设置。
梯度近似软函数会增加大量的训练时间。
对比每个二值算法的训练开销,本文发现,使用了自定义梯度近似技术的算法,例如Bi-Real和ReActNet算法,它们的训练时间有显著的增加,而 FDA的训练时间甚至几乎是全精度模型的5倍。
理论复杂度
不同的二值模型的算法的理论复杂度并没有明显的不同。
不同算法间压缩率差异的主要原因在于每个模型的缩放因子的定义方式不同,例如,BNN 没有缩放因子。
对于理论加速情况,二值算法间的主要区别来自两个方面。首先,静态的缩放因子的压缩也提高了理论加速比。
其次,对于激活值实时的缩放和均值偏移会带来额外的理论计算,例如ReActNet,能够减少0.11×的加速。
但是总的来说,本文的实验表明,各种二值化算法具有相似的理论推理效率。
硬件推理
相比于其他的轨道,“硬件推理”轨道能够提供一些二值算法在真实世界部署的启示。

极其有限的推理库导致了几乎固定的二值化部署范式。
在调查了现有开源推理框架之后,本文发现能够支持二值模型在真实硬件上部署的推理库非常少。只有Larq和daBNN拥有完整的二值化算法部署流程,它们主要支持在ARM设备上进行部署。
首先验证这两个推理库的部署能力,结果呈现在表4中。两个推理库都支持逐通道的浮点缩放因子,并强制将它融合进BN层,此外,二者都不支持动态激活缩放。
它们唯一的区别是,Larq能支持激活值基于固定值的偏移。
由于推理库的部署限制,能够实际部署的二值算法是有限的。XNOR++使用的缩放因子是不能部署的,XNOR的激活动态缩放也是不支持的。
除了ReActNet所使用的激活均值偏移会增加少量的计算量,其他能够部署的二值算法,大多具有几乎完全相同的推理表现。
也就是说,二值算法必须能够满足固定的部署范式才能够使用现有的推理库成功部署,并且它们在硬件上具有几乎相同的表现。

△ 图3: 二值算法在算力越低的硬件芯片上能够达到越高的推理加速比
为边缘而生:芯片的算力越低,二值化模型的加速比越高。
BiBench部署和评估了十几个芯片上的二值化模型,并比较了每个芯片上二值化算法的平均加速比。
图3中呈现了一个反直觉的规律:芯片的算力性能越高,二值化模型的加速比越低。
通过进一步观察,本文发现这主要是因为多线程计算。性能更好的芯片在运行浮点计算时使用了更多线程的并行,能够带来显著的浮点运算加速。
因此,相比之下,二值化模型的加速并不明显。
这意味着二值化技术真正发挥作用的场景,是在算力性能和成本较低的边缘芯片上,而二值化所带来的极限压缩和加速可以促进人工智能模型在此类边缘芯片上的运行。
关于二值算法设计的一些建议
基于上述的验证和分析,本文试图从现有的二值技术中,总结一些准确高效的二值算法的设计范式:
(1) 软量化近似是二值化的一个必要的技术。它不会影响模型在硬件推理时的高效性,所有在准确率轨道上表现优秀的算法都采用了这个技术,包括Bi-Real、ReActNet和ReCU。
(2) 逐通道缩放因子是考虑可部署性的唯一选择。在任务和架构两轨道上的准确率结果说明了浮点缩放因子的优势,而现有推理库在硬件上的实际部署能力又限制了缩放因子必须是逐通道的形式。
(3) 对激活值的均值偏移是一个有助于准确率提升的可选项。本文结果表明这项技术有助于ReActNet准确率的提升,并且几乎没有额外的计算开销。
需要强调的是,虽然BiBench所包含的六个轨道能够帮助找到一些二值网络设计的基本原则,但是没有哪个算法能在所有场景下都具有优势。
未来的二值化算法研究应侧重于打破生产与部署之间的互相限制。二值算法应遵循可部署的原则进行设计,而推理库应当尽可能地支持先进的更高精度的二值算法。
总结
本文提出了一个全面的多功能的二值算法基准框架BiBench,深入地研究了二值算法的最基本的问题。
BiBench覆盖了8种模型二值化算法、13种网络架构、9个深度学习数据集,14种真实世界的硬件,以及多种超参数设置。
此外,BiBench针对一些关键的特性专门设计了评测的轨道,例如在不同条件下的算法准确性以及在真实硬件上部署时的高效性。
更重要的是,通过整理、总结和分析实验结果,BiBench希望能够建立一些经验性的设计范式,其中包含设计准确有效的二值化方法的几个关键考虑因素。
研究人员希望,BiBench能够通过系统性的研究反映模型二值领域的现实需求,促进算法的公平比较,并作为在更广泛和更实际的背景下应用模型二值化的基础。




