2022年,前谷歌大脑华人科学家Jason Wei在一篇思维链的开山之作中首次提出,CoT可以增强LLM的推理能力。
但即便有了思维链,LLM有时也会在非常简单的问题上犯错。
最近,来自普林斯顿大学和Google DeepMind研究人员提出了一种全新的语言模型推理框架——「思维树」(ToT)。
ToT将当前流行的「思维链」方法泛化到引导语言模型,并通过探索文本(思维)的连贯单元来解决问题的中间步骤。

论文地址:https://arxiv.org/abs/2305.10601
项目地址:https://github.com/kyegomez/tree-of-thoughts
简单来说,「思维树」可以让LLM:
· 自己给出多条不同的推理路径
· 分别进行评估后,决定下一步的行动方案
· 在必要时向前或向后追溯,以便实现进行全局的决策
论文实验结果显示,ToT显著提高了LLM在三个新任务(24点游戏,创意写作,迷你填字游戏)中的问题解决能力。
比如,在24点游戏中,GPT-4只解决了4%的任务,但ToT方法的成功率达到了74%。
让LLM「反复思考」
用于生成文本的大语言模型GPT、PaLM,现已经证明能够执行各种广泛的任务。
所有这些模型取得进步的基础仍是最初用于生成文本的「自回归机制」,以从左到右的方式一个接一个地进行token级的决策。

那么,这样一个简单的机制能否足以建立一个通向「解决通用问题的语言模型」?如果不是,哪些问题会挑战当前的范式,真正的替代机制应该是什么?
恰恰关于「人类认知」的文献为这个问题提供了一些线索。
「双重过程」模型的研究表明,人类有两种决策模式:快速、自动、无意识模式——「系统1」和缓慢、深思熟虑、有意识模式——「系统2」。

语言模型简单关联token级选择可以让人联想到「系统1」,因此这种能力可能会从「系统2」规划过程中增强。
「系统1」可以让LLM保持和探索当前选择的多种替代方案,而不仅仅是选择一个,而「系统2」评估其当前状态,并积极地预见、回溯以做出更全局的决策。
为了设计这样一个规划过程,研究者便追溯到人工智能和认知科学的起源,从科学家Newell、Shaw和Simon在20世纪50年代开始探索的规划过程中汲取灵感。
Newell及其同事将问题解决描述为「通过组合问题空间进行搜索」,表示为一棵树。
一个真正的问题解决过程包括重复使用现有信息来探索,反过来,这将发现更多的信息,直到最终找到解决方法。

这个观点突出了现有使用LLM解决通用问题方法的2个主要缺点:
1. 局部来看,LLM没有探索思维过程中的不同延续——树的分支。
2. 总的来看,LLM不包含任何类型的计划、前瞻或回溯,来帮助评估这些不同的选择。
为了解决这些问题,研究者提出了用语言模型解决通用问题的思维树框架(ToT),让LLM可以探索多种思维推理路径。
ToT四步法
当前,现有的方法,如IO、CoT、CoT-SC,通过采样连续的语言序列进行问题解决。
而ToT主动维护了一个「思维树」。每个矩形框代表一个思维,并且每个思维都是一个连贯的语言序列,作为解决问题的中间步骤。

ToT将任何问题定义为在树上进行搜索,其中每个节点都是一个状态,表示到目前为止输入和思维序列的部分解。
ToT执行一个具体任务时需要回答4个问题:
如何将中间过程分解为思维步骤;如何从每个状态生成潜在的想法;如何启发性地评估状态;使用什么搜索算法。
1. 思维分解
CoT在没有明确分解的情况下连贯抽样思维,而ToT利用问题的属性来设计和分解中间的思维步骤。
根据不同的问题,一个想法可以是几个单词(填字游戏) ,一条方程式(24点) ,或者一整段写作计划(创意写作)。
一般来说,一个想法应该足够「小」,以便LLM能够产生有意义、多样化的样本。比如,生成一本完整的书通常太「大」而无法连贯 。
但一个想法也应该「大」,足以让LLM能够评估其解决问题的前景。例如,生成一个token通常太「小」而无法评估。
2. 思维生成器
给定树状态 ,通过2种策略来为下一个思维步骤生成k个候选者。
,通过2种策略来为下一个思维步骤生成k个候选者。
(a)从一个CoT提示采样![]() 思维:
思维:
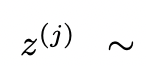

在思维空间丰富(比如每个想法都是一个段落),并且![]() 导致多样性时,效果更好。
导致多样性时,效果更好。
(b)使用「proposal prompt」按顺序提出想法:
。这在思维空间受限制(比如每个思维只是一个词或一行)时效果更好,因此在同一上下文中提出不同的想法可以避免重复。
3. 状态求值器

给定不同状态的前沿,状态评估器评估它们解决问题的进展,作为搜索算法的启发式算法,以确定哪些状态需要继续探索,以及以何种顺序探索。
虽然启发式算法是解决搜索问题的标准方法,但它们通常是编程的(DeepBlue)或学习的(AlphaGo)。这里,研究者提出了第三种选择,通过LLM有意识地推理状态。
在适用的情况下,这种深思熟虑的启发式方法可以比程序规则更灵活,比学习模型更有效率。与思维生成器,研究人员也考虑2种策略来独立或一起评估状态:对每个状态独立赋值;跨状态投票。
4. 搜索算法
最后,在ToT框架中,人们可以根据树的结构,即插即用不同的搜索算法。
研究人员在此探索了2个相对简单的搜索算法:
算法1——广度优先搜索(BFS),每一步维护一组b最有希望的状态。
算法2——深度优先搜索(DFS),首先探索最有希望的状态,直到达到最终的输出,或者状态评估器认为不可能从当前的为阈值解决问题。在这两种情况下,DFS都会回溯到s的父状态以继续探索。

由上,LLM通过自我评估和有意识的决策,来实现启发式搜索的方法是新颖的。
实验
为此,团队提出了三个任务用于测试——即使是最先进的语言模型GPT-4,在标准的IO提示或思维链(CoT)提示下,都是非常富有挑战的。

24点(Game of 24)
24点是一个数学推理游戏,目标是使用4个数字和基本算术运算(+-*/)来得到24。
例如,给定输入「4 9 10 13」,答案的输出可能是「(10-4)*(13-9)=24」。
ToT设置
团队将模型的思维过程分解为3个步骤,每个步骤都是一个中间方程。
如图2(a)所示,在每个节点上,提取「左边」的数字并提示LLM生成可能的下一步。(每一步给出的「提议提示」都相同)
其中,团队在ToT中进行宽度优先搜索(BFS),并在每一步都保留最好的b=5个候选项。
如图2(b)所示,提示LLM评估每个思维候选项是「肯定/可能/不可能」达到24。基于「过大/过小」的常识消除不可能的部分解决方案,保留剩下的「可能」项。
结果
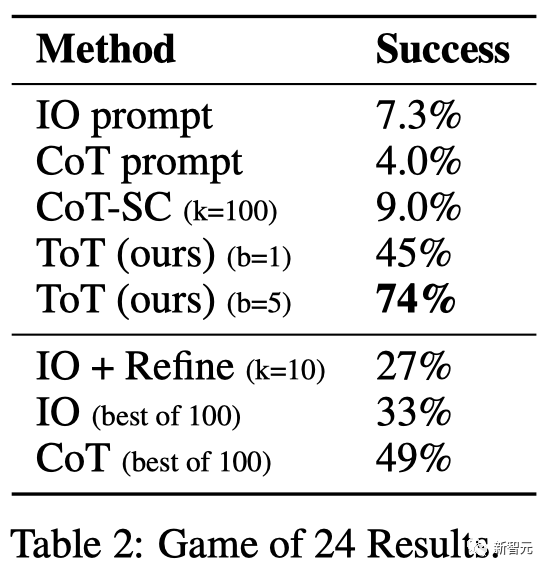
如表2所示,IO,CoT和CoT-SC提示方法在任务上的表现不佳,成功率仅为7.3%,4.0%和9.0%。相比之下,ToT在广度为b=1时已经达到了45%的成功率,而在b=5时达到了74%。
团队还考虑了IO/CoT的预测设置,通过使用最佳的k个样本(1≤k≤100)来计算成功率,并在图3(a)中绘出5个成功率。
不出所料,CoT比IO扩展得更好,最佳的100个CoT样本达到了49%的成功率,但仍然比在ToT中探索更多节点(b>1)要差。
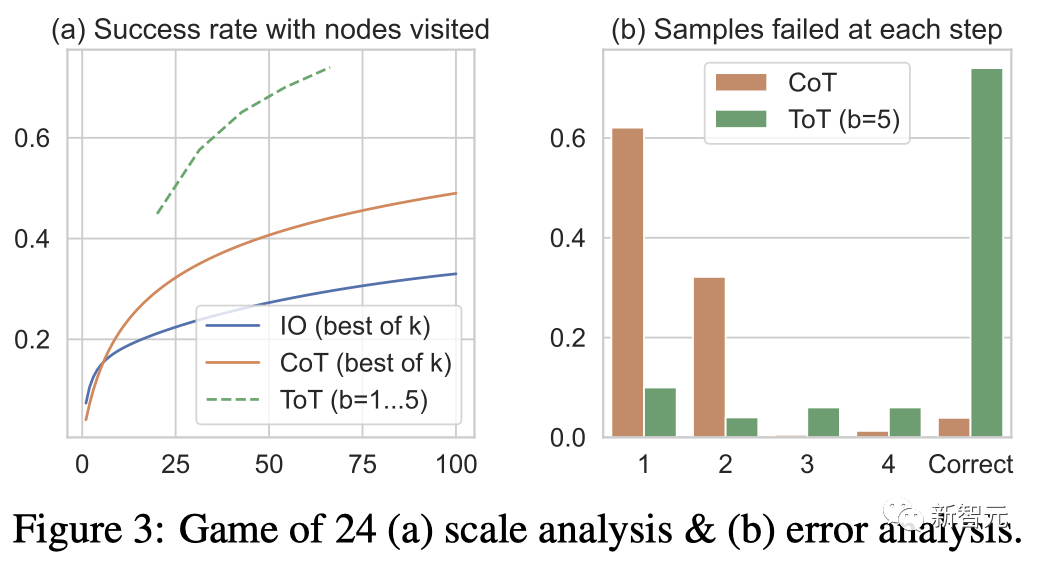
错误分析
图3(b)分析了CoT和ToT样本在哪一步失败了任务,即思维(在CoT中)或所有b个思维(在ToT中)都是无效的或无法达到24。
值得注意的是,大约60%的CoT样本在第一步就已经失败了,或者说,是前三个词(例如「4+9」)。
创意写作
接下来,团队设计了一个创意写作任务。
其中,输入是四个随机句子,输出应该是一个连贯的段落,每段都以四个输入句子分别结束。这样的任务开放且富有探索性,挑战创造性思维以及高级规划。
值得注意的是,团队还在每个任务的随机IO样本上使用迭代-优化(k≤5)方法,其中LLM基于输入限制和最后生成的段落来判断段落是否已经「完全连贯」,如果不是,就生成一个优化后的。
ToT设置
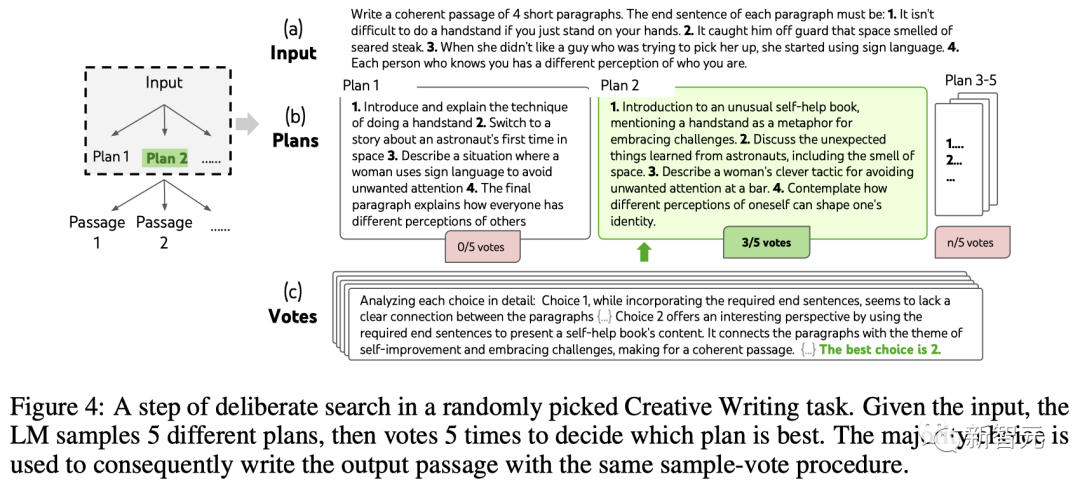
团队构建了一个深度为2(只有1个中间思维步骤)的ToT。
LLM首先生成k=5的计划并投票选择最佳的一个(图4),然后根据最佳计划生成k=5的段落,然后投票选择最佳的一个。
一个简单的zero-shot投票提示(「分析以下选择,然后得出哪个最有可能实现指令」)被用来在两个步骤中抽取5票。
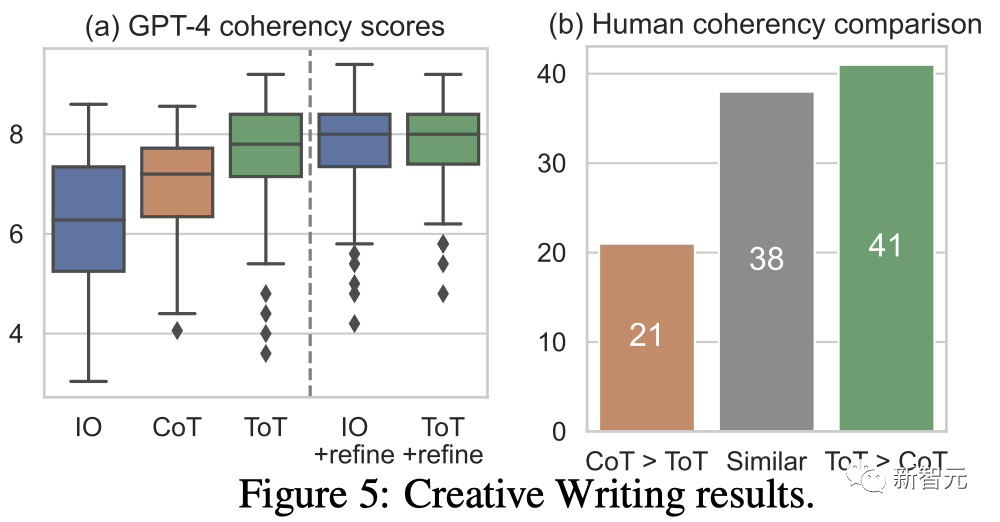
结果
图5(a)显示了100个任务中的GPT-4平均分数,其中ToT(7.56)被认为比IO(6.19)和CoT(6.93)平均生成更连贯的段落。
虽然这样的自动评测可能会有噪音,但图5(b)通过显示人类在100个段落对中有41个更喜欢ToT而只有21个更喜欢CoT(其他38对被认为「同样连贯」)来确认这一发现。
最后,迭代优化在这个自然语言任务上更有效——将IO连贯性分数从6.19提高到7.67,将ToT连贯性分数从7.56提高到7.91。
团队认为它可以被看作是在ToT框架下生成思维的第三种方法,新的思维可以通过优化旧的思维而产生,而不是i.i.d.或顺序生成。
迷你填字游戏
在24点游戏和创意写作中,ToT相对较浅——最多需要3个思维步骤就能完成输出。
最后,团队决定通过5×5的迷你填字游戏,来设置一个更难的问题。
同样,目标不仅仅是解决任务,而是研究LLM作为一个通用问题解决者的极限。通过窥视自己的思维,以有目的性的推理作为启发,来指导自己的探索。

ToT设置
团队利用深度优先搜索保持探索最有可能成功的后续单词线索,直到状态不再有希望,然后回溯到父状态以探索替代的思维。
为了使搜索可行,后续的思维被限制不改变任何已填写的单词或字母,这样ToT最多有10个中间步骤。
对于思维生成,团队在每个状态下将所有现有的思维(例如,「h2.motor; h1.tasks」对于图6(a)中的状态)转换为剩余线索的字母限制(例如,「v1.To heap: tm___;…」),从而得到下一个单词填写位置和内容的候选。
重要的是,团队也提示LLM给出不同思维的置信度,并在提案中汇总这些以获得下一个要探索的思维的排序列表(图6(a))。
对于状态评估,团队类似地将每个状态转换为剩余线索的字母限制,然后评估每个线索是否可能在给定限制下填写。
如果任何剩余的线索被认为是「不可能」的(例如,「v1. To heap: tm_s_」),那么该状态的子树的探索就被剪枝,并且DFS回溯到其父节点来探索下一个可能的候选。

结果
如表3所示,IO和CoT的提示方法在单词级成功率上表现不佳,低于16%,而ToT显著改善了所有指标,实现了60%的单词级成功率,并解决了20个游戏中的4个。
鉴于IO和CoT缺乏尝试不同线索、改变决策或回溯的机制,这种改善并不令人惊讶。
局限性与结论
ToT是一个让LLM可以更自主、更智能地做决策和解决问题的框架。
它提高了模型决策的可解释性以及与人类对齐的机会,因为ToT所生成的表征表形式是可读的、高级的语言推理,而不是隐式的、低级的token值。
对于那些GPT-4已经十分擅长的任务来说,ToT可能并是不必要的。
此外,像ToT这样的搜索方法需要更多的资源(如GPT-4 API成本)来提高任务性能,但ToT的模块化灵活性让用户可以自定义这种性能-成本平衡。
不过,随着LLM被用于更多真实世界的决策应用(如编程、数据分析、机器人技术等),ToT可以为研究那些即将出现的更为复杂的任务,提供新的机会。
作者介绍
Shunyu Yao(姚顺雨)

论文一作Shunyu Yao是普林斯顿大学的四年级博士生,此前毕业于清华大学的姚班。
他的研究方向是在语言智能体与世界之间建立互动,例如玩文字游戏(CALM),网上购物(WebShop),浏览维基百科进行推理(ReAct),或者,基于同样的想法,用任何工具来完成任何任务。
在生活中,他喜欢阅读、篮球、台球、旅行和说唱。
Dian Yu

Dian Yu是Google DeepMind的一名研究科学家。此前,他在加州大学戴维斯分校获得了博士学位,并在纽约大学获得了学士学位,双主修计算机科学和金融(还有一点表演)。
他的研究兴趣是语言的属性表征,以及多语言和多模态的理解,主要专注于对话研究(包括开放领域和任务导向)。
Yuan Cao
Yuan Cao也是Google DeepMind的一名研究科学家。此前,他在上海交通大学获得了学士和硕士学位,并在约翰斯·霍普金斯大学获得了博士学位。还曾担任过百度的首席架构师。
Jeffrey Zhao

Jeffrey Zhao是Google DeepMind的软件工程师。此前,他在卡内基梅隆大学获得了学士和硕士学位。



